În secțiunea anterioară momentului de inerție a fost determinată ca masa totală a pătratelor elementare distanțele lor față de axa [vezi. (38.2)]. Definiția sugerează faptul că momentul de inerție este aditiv. Aceasta înseamnă că momentul de inerție este egal cu suma momentelor de inerție ale pieselor.
Distribuția masei în interiorul corpului poate fi caracterizată printr-o valoare numită densitate. În cazul în care corpul este omogen, adică proprietăți. E. sale la toate punctele de aceeași, densitatea este o cantitate egală cu
unde m este masa corpului, iar V - volumul său. Astfel, în cazul unei densitate uniformă a corpului este masa corporală per unitate de volum.
Pentru corp cu ecuația de masă distribuite neuniform (39,1) dă densitatea medie. densitatea la un moment dat, în acest caz, este definită după cum urmează:
Integralele din (39.5) sunt luate în jurul volumului corp. valoare # 961; și r sunt integralele în aceste funcții ale punctului, t. e. de exemplu, coordonatele x cartezian, y și z.
Ca exemplu, vom găsi momentul disc omogen de inerție față de o axă perpendiculară pe planul discului și care trece prin centrul său (Figura 102).
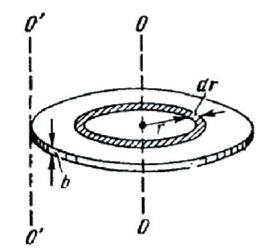
Am împărți discul în straturi groase dr inelare. Toate punctele de un singur strat va fi la aceeași distanță față de axa egală cu r. Volumul de astfel de strat este
unde b - grosimea discului.
Deoarece discul este uniformă, densitatea acestuia este aceeași la toate punctele, și # 961; în (39.5) pot fi luate în afara semnului integrală:
unde R - raza discului. Luate în afara integrantă factor 2πb constant:
În final, introduceți masa m disc, egală cu densitatea # 961; pe cantitatea de disc bπR 2. obține:
Determinarea momentului de inerție în acest exemplu este simplificat în mod considerabil prin faptul că organismul este uniform și simetric, și am căutat momentul de inerție în raport cu axa de simetrie. Dacă ne-am dorit să găsim pentru momentul de inerție al discului în ceea ce privește, de exemplu, axa O'o“perpendiculară pe disc și care trece prin teritoriul său (a se vedea. Fig. 102), de calcul, în mod evident, ar fi fost mult mai complexe. In astfel de cazuri, găsirea momentului de inerție este mult ușurată dacă utilizarea Teorema Steiner, care este formulat după cum urmează: momentul de inerție I față de o axă arbitrară este suma momentului de I0 inerție în raport cu o axă paralelă cu aceasta și carcase care se extind din centrul corpului în masă, iar produsul de m greutate corporală pe pătratul distanței și între axe:
În conformitate cu teorema lui Steiner momentul de inerție în raport cu axa discului O'O "ranit gasit punctul de contact inerție (39.6) în jurul unei axe care trece prin centrul discului plus mR 2 (distanța dintre axele O'O și ale discului OO egale cu raza R):
Astfel Teorema Steiner reduce substanțial calculul momentului de inerție față de o axă arbitrară calcularea momentului de inerție față de o axă care trece prin centrul de masă al corpului.
Pentru a demonstra aceasta teorema lui considerăm corpul Steiner de forma arbitrara (Fig. 103) Luarea în considerare două axe paralele și OO O'O „dintre care unul (G-axa) trece prin centrul de masă al corpului. Asociat cu aceste axe xyz axele de coordonate și x'y „z“, sunt alese astfel încât axa z coincide cu axa OO, iar axa z „- axa cu O'O“ (. 103 din Fig aceste axe sunt perpendiculare pe planul desenului) .
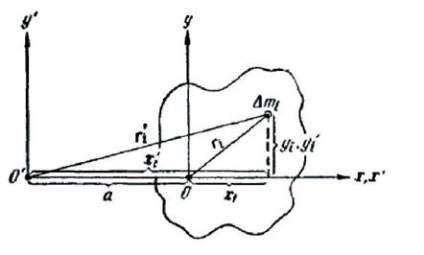
În plus, X și X „sunt alese astfel încât acestea să coincidă și să treacă prin centrul de masă al corpului. Apoi, între coordonatele elementare în masă # 916; postinfarct va avea următoarele relații:
unde a - distanța dintre axele.
pătratul distanței # 916; mi este de la axa OO
pătratul distanței de la axa O'O „este
În ceea ce privește (39,8), momentul de inerție în raport cu axa OO este dată de
și momentul de inerție în jurul axei O'O „[considerând (39,9)] este egal cu
Cvadratura expresia în paranteze și grupați termenii corespunzător care rezultă, expresia (39,11) poate fi redus la forma:
Prima sumă (39.12) identică cu (39.10), adică I este 0 ..; a doua sumă dă 2 ma treia sumă aceeași, așa cum este ușor de văzut, este egal cu zero. De fapt, deoarece axa z trece prin centrul de masă al corpului, cu x coordonata centrului de masă este zero. Cu toate acestea, prin definiție. ceea ce implică faptul că zero.
Astfel, ecuația (39.12) ia forma
QED [vezi. (39,7)].
In concluzie, prezentăm valorile pentru momentul de inerție al unor corpuri (corp presupuse a fi omogene, m - greutate).
1. Corpul este o tijă lungă și subțire, cu o secțiune transversală de orice formă. Dimensiunea transversală maximă b a tijei este mult mai mică decât lungimea
tijă l (b <

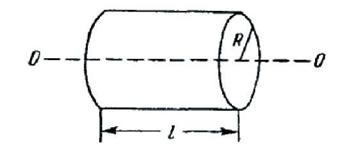
2. Pentru un disc sau cilindru, în orice raport R la l (Fig. 105) moment de inerție în jurul unei axe care coincide cu axa geometrică a cilindrului este egală cu
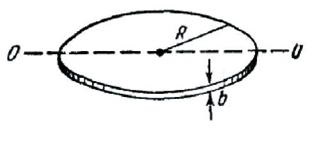
3. Corpul - Discul subțire. Disk B grosime de multe ori mai mică decât raza discului R (b <
4. Momentul de inerție bilă de rază R în jurul unei axe ce trece prin centrul său, este egal cu