Toate posibilele cazuri de poziție reciprocă a liniei și planul în spațiu:
1. minciuni directe în plan (planul aparține)
Linia se află pe planul în cazul în care toate punctele de linie aparțin avionului.
Notă. Pentru a pune direct pe planul, este necesar și suficient ca oricare două puncte ale acestei linii a aparținut acestui plan.
2. Linia intersectează planul
Linia intersectează planul, în cazul în care o linie și un plan au un singur punct comun
3. plan paralel directă
paralelă directă cu planul, în cazul în care linia dreaptă și planul nu au puncte comune. (Ei nu se suprapun
Propoziția 1. Să presupunem că linia dreaptă și un plan paralel cu α, p și planul trece prin linia a. Apoi, există două posibilități:
- Β plan paralel cu planul subunitatea;
- Β planul intersectează planul a. În acest caz, linia b, care este linia de intersecție a avioanelor a și β, ar fi paralelă cu linia a.


Dovada. Luați în considerare cazul 2 și să își asume contrariul. Să presupunem că liniile a și b se intersectează într-un punct P.
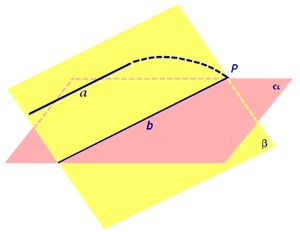
Dar, în cazul în care punctul P este punctul de intersecție al liniei și un plan α. și obținem o contradicție cu faptul că liniile a și α planul paralel. Această contradicție completează dovada Propoziția 1.
Adoptarea 2 (semn linie paralelă și un avion). În cazul în care linia dreaptă a. care nu se află în planul α. paralel cu o linie dreaptă b. situată în planul α. apoi o linie dreaptă și paralelă cu planul α.
Dovada. Demonstrăm un semn de paralelism de linie dreaptă și planul „de contradicție“. Să presupunem că un plan α dreaptă se intersectează într-un punct P. Egal plan β prin linii paralele a și b.

Punctul P se află pe un plan β și aparține. Cu toate acestea, prin punctul P presupunere aparține și planul a. deci punctul P se află pe linia b, din care se intersectează și subunitatea p plane. Cu toate acestea, o directă și b sunt paralele cu condiția și poate avea niciun punct comun.
Această contradicție completează dovada caracteristicii de linii paralele și avioane.
- În cazul în care o linie care intersectează un plan perpendicular pe cele două linii drepte situate în acest plan și care trece prin punctul de intersecție al liniei și planul, este perpendicular pe planul.
- Dacă planul este perpendicular pe una din cele două linii paralele, este perpendicular pe cealaltă.
- Dacă două linii sunt perpendiculare pe același plan, atunci ele sunt paralele.
- În cazul în care o linie situată într-un plan perpendicular pe proiecția unui înclinat, atunci este perpendiculară și cea mai înclinată.
- În cazul în care o linie nu se află în planul paralel cu oricare linie dreaptă situate în acest plan, este paralelă cu acest plan.
- În cazul în care linia este paralelă cu un plan care este paralel cu o linie dreaptă în avion.
- Dacă o linie dreaptă și un plan perpendicular pe aceeași linie dreaptă, atunci ele sunt paralele.
- Toate punctele de pe linia paralelă cu planul echidistant față de acest plan.
Întrebări pentru rezumate
Plane α, paralelă cu latura BC a triunghiului ABC intersectează laturile AB și AC în punctele M și N, respectiv. Găsiți segmentul BC lungime dacă MN = 6 cm și AM: CF = 3: 5
Plan α, laterale paralele KL CKL triunghi intersectează LC și mâna KS la punctele P și D, respectiv. Găsiți lungimea PD segmentului, dacă KL = 27 cm, și uscat: DC = 7: 2