Descriere: Ecuația diferențială a ecuației privind valoarea unor funcții necunoscute la un moment dat și valoarea derivatelor sale de ordine diferite în același punct. Ecuația diferențială conține funcția necunoscută și derivații săi sunt variabilele independente într-o legătură; dar care nu conține nici o ecuație derivată funcție necunoscută este o ecuație diferențială. Ecuația diferențială neliniară, sau o ecuație diferențială ordinară de derivate parțiale în care cel puțin unul.
Dimensiune fișier: 163.25 KB
Job descărcat: 39 de persoane.
Dacă această lucrare au ajuns în partea de jos a paginii există o listă de lucrări similare. De asemenea, puteți folosi butonul de căutare
PSU numit. TG Shevchenko
Tipuri de ecuații diferențiale neliniare de ordinul 1
211 grupuri de studenți
Igor A. Birt
1. Introducere pagina 3.
2. Tipuri de ecuatii diferentiale 4 p.
3. Partea practică 8 puncte procentuale.
4. Referințe 20 p.
ecuație diferențială # 151; ecuația privind valoarea unor funcții necunoscute la un moment dat și valoarea derivatelor sale de ordine diferite în același punct. Ecuația diferențială conține funcția necunoscută, derivații săi și variabilele independente într-o legătură; dar nu orice ecuație care conține derivați de funcție necunoscută, este o ecuație diferențială.
Ordinea ecuației diferențiale # 151; cel mai înalt ordin al instrumentelor derivate incluse în ea.
Procesul de rezolvare a unei ecuații diferențiale se numește integrare.
Toate ecuațiile diferențiale pot fi împărțite în liniare și neliniare.
Ecuația diferențială neliniară - ecuația diferențială (obișnuită sau parțială) a unui GR Roe, cel puțin pe partea de jos a derivaților funcției necunoscute (inclusiv derivatul de ordinul zero - în sine funcție necunoscută) include nonlinearly.
Uneori, sub N.D.U. Aceasta se referă la ecuația cea mai generală a unui anumit tip. Ex. ecuație diferențială nelineynymobyknovennym 1 - ordinea numită. ecuație cu arbitrară
funcție cu ecuația diferențială ordinară liniară de ordinul 1 corespunde cazului particular
N. d. Y. Prima comandă parțială pentru funcția necunoscută z
variabilele independente este după cum urmează:
în cazul în care F - funcție arbitrară a argumentelor sale;
Tipuri de ecuații diferențiale neliniare de ordinul 1:
Ecuații cu variabile separate
ecuație diferențială ordinară
Există o funcție u (x, y). că
totală Integrala din ecuație diferențială completă u (x, y) = C.
Funcția u poate fi reprezentat sub forma
unde P (x, y). Q (x, y) - funcția omogenă în aceeași măsură
Substituind y = ux. dy = xdu + udx ecuație omogenă se traduce printr-o funcție liniară în raport cu u.
1. În cazul în care liniile și se intersectează într-un punct
(X 0; y 0), înlocuindu-l conduce la o ecuație omogenă
2. Dacă calea cea dreaptă paralelă, înlocuirea conduce la o ecuație cu variabile multiple
Schimbare reduce la liniar
Dacă știți oricare dintre deciziile. ecuația se reduce la
Diferențierea în ceea ce privește x și presupunând că y „= p. Am ajuns la o ecuație liniară pentru x în funcție de p.
- un caz particular al ecuațiilor Lagrange.
Pentru a rezolva ecuația diferențială
Această ecuație este cea mai simplă ecuația Riccati cu coeficienți constanți. Variabilele x, y sunt separate cu ușurință, astfel încât soluția generală este definită după cum urmează:

Rezolva ecuația Riccati
Noi căutăm o soluție special sub formă de:
Substituind acest lucru în ecuație, găsim:
Obținem o ecuație pătratică pentru c:
Putem alege orice valoare c. De exemplu, să presupunem că c = 2. Acum, că știi o soluție anume, vom face schimbarea:
Din nou înlocuim acest lucru în ecuația Riccati originală:
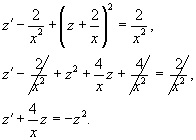
După cum puteți vedea, avem o ecuație Bernoulli cu parametrul m = 2. Să facem o altă schimbare:
Se împarte ecuația Bernoulli pentru z2 (presupunând că z ≠ 0) și scrie-l prin variabila v:
Ultima ecuație este liniară și poate fi rezolvată ușor prin utilizarea unui factor de integrare:
Soluția generală a ecuației liniare determinată de funcția
Acum, vom reveni în mod constant la variabilele anterioare. Deoarece z = 1 / v, soluția generală pentru z este scris după cum urmează:
Puteți redenumi o constantă: 3C = C1 și scrie răspunsul în formă de
unde C1 - număr real arbitrar.
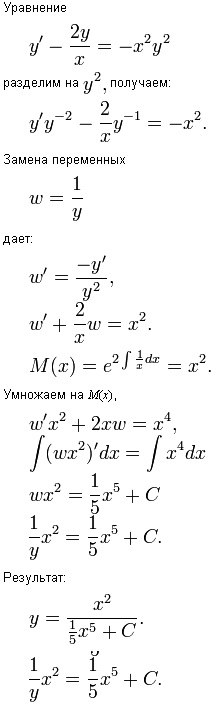
Găsiți toate soluțiile ecuației diferențiale
Această ecuație este un parametru fracționată Bernoulli
m = 1/2. Acesta poate fi redusă la o ecuație diferențială liniară prin înlocuirea
Derivata nouă funcție z (x) este egal cu
Noi împărțim ecuația lui Bernoulli originală pentru
În mod similar, alte exemple de pe această pagină web, rădăcina y = 0 este de asemenea o soluție trivială a ecuației diferențiale. Prin urmare, putem scrie:
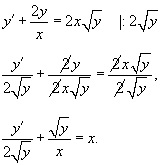
Substituind pentru y z. am găsit:
Deci, avem o ecuație liniară pentru z funcția (x). factor integrator aici este egal cu
Am ales ca funcție factor de integrare u (x) = x. Este posibil să se verifice dacă, după înmulțirea cu u (x) din partea stângă a ecuației va fi o lucrare derivată z (x) u (x):
Apoi, soluția generală a ecuației diferențiale liniare este determinată de expresia:
Revenind la funcția inițială y (x), vom scrie soluția în formă implicită:
Deci, un răspuns complet este după cum urmează:
Ecuatii cu variabile separabile
Găsiți toate soluțiile ecuației diferențiale
Transformare ecuație după cum urmează:
Este evident că împărțirea în e y nu există soluții de pierdere ca e y> 0. După integrare obținem
Acest răspuns poate fi exprimat în mod explicit:
În ultima expresie se presupune că o C constantă> 0, pentru a satisface domeniul functiei logaritmice.
Găsiți o soluție specială, atunci când
Rescriem ecuația după cum urmează:
Se împarte ambele părți cu 1 + e x.
De la 1 + e x> 0, atunci divizia nu am pierdut orice decizii. Integrarea ecuația rezultată este:
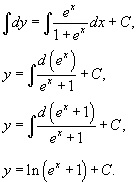
Acum vom găsi constanta C de la condiția inițială y (0) = 0.
Prin urmare, răspunsul final este:
Găsiți soluțiile generale și particulare ale ecuației diferențiale
Presupunând că y „= p, acesta poate fi scris ca
Diferențierea în ceea ce privește x, găsim:
Înlocuiți DY pe PDX:
Asimilarea primul factor la zero, obținem:
Acum substituie acest lucru în a doua ecuație:
Ca rezultat, vom obține soluția generală a ecuației dată de Clairout. Grăitor, această soluție este reprezentată ca o familie, un parametru de linii drepte. Asimilarea la zero al doilea factor, vom găsi o altă soluție:
Această ecuație corespunde unei soluții particulare a ecuației diferențiale și o formă parametrică este scrisă ca
Eliminarea p din sistem, următoarea ecuație curba integrală:
Din punct geometric de vedere, parabolei
Este anvelopa unei familii de linii drepte definite de soluția generală.
Găsiți soluțiile generale și particulare ale ecuației diferențiale
Introducem parametrul y „= p:
Diferențierea ambele părți în raport cu x a ecuației, obținem:
Deoarece dy = PDX, putem scrie:
Să considerăm cazul dp = 0. Atunci p = C. Înlocuind aceasta în ecuație, găsi soluția generală:
Grăitor, această soluție corespunde unei familii un parametru de linii drepte.
Al doilea caz este descris de ecuația
Găsiți expresia parametric corespunzătoare pentru y:
Parametrul p poate fi omisă din formulele pentru x și y. Ridicarea ultima ecuație în piață și adăugarea lor, obținem:
Expresia rezultată este ecuația unui cerc cu raza de 1, situat la origine. Astfel, o soluție specială este reprezentată de cercul unitate din xy plan, care este înfășurătoarea familiei de linii drepte.
- NS Piskunov "calcul diferențial și integral", Volumul doi, "Nauka", București 1985
- E. Kamke. Manualul de ecuații diferențiale ordinare. M. Science, 1976.
- Surse de informații pe Internet.
PAGE \ * MERGEFORMAT 19