În acest articol vă voi arăta cum să genereze numere aleatoare folosind patru algoritmi diferite: Lehmer algoritm (Lehmer), algoritmul congruential liniar (algoritmul congruential liniar), algoritmul Wichmann-Hill (Wichmann-Hill), iar algoritmul lui Fibonacci Delay (ramas algoritmul lui Fibonacci) .
Dar de ce povara le crea propriul generator de numere aleatorii (generator de numere aleatorii, RNG), atunci când Microsoft .NET Framework este deja un sistem eficient și ușor de utilizat clasa aleatorie? Există două scenarii în cazul în care s-ar putea nevoie pentru a crea propriul RNG. În primul rând, în diferite limbaje de programare sunt construite diferite algoritmi pentru generarea de numere aleatoare, ceea ce înseamnă că, dacă scrieți cod care va fi transferat în mai multe limbi, puteți crea propriul RNG, să-l pună în aplicare în toate limbile pe care le doriți. În al doilea rând, unele limbi, cum ar fi R, au doar la nivel mondial RNG-ul, deci, dacă doriți să creați mai multe generatoare, trebuie să scrie RNG ta.
O modalitate bună de a obține o idee de unde am de gând în acest articol - uita-te la programul de exemplu în Fig. 1. program demonstrativ începe prin crearea unui RNGYU foarte simplu, folosind Lehmer algoritm. Apoi, folosind RNG 1000 generează numere aleatoare între 0 și 9 inclusiv. În spatele scenei contoare pentru fiecare dintre numerele întregi generate, care sunt apoi afișate pe ecran înregistrate. Acest procedeu se repetă pentru un algoritm congruential Wichmann-Hill algoritm liniar și întârzieri algoritmul lui Fibonacci.
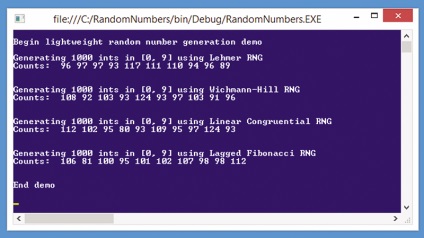
Fig. 1. Demonstrarea de generare simplificată de numere aleatoare
Acest articol presupune că știi cum să programeze cel puțin la nivelul mediu, dar nu știu nimic despre generarea de numere aleatoare. Programul demonstrativ este scris în C #, ci ca una dintre principalele utilizări ale propriei generație de numere aleatorii - scrierea de cod portabil, programul este conceput astfel încât să poată fi ușor de tradus în alte limbi.
Lehmer algoritm
Cea mai simplă metodă este adecvată pentru generarea de numere aleatoare - Lehmer algoritm. (Pentru simplificare, folosesc termenul de „generare de numere aleatorii“ în locul termenului mai precis „generare de numere aleatorii“.) Exprimat în mod simbolic, Lemaire algoritm este după cum urmează:
În cuvinte, se pare ca acest lucru: „un nou număr aleator este numărul vechi aleatoriu este înmulțită cu o constantă, atunci rezultatul operației se efectuează modulo constantele m». De exemplu, să presupunem că la un moment dat numărul aleatoriu curent este egal cu 104, o = 3 și m = 100. Apoi, un nou număr aleator este egal cu 3 * 104 mod 100 = 312 mod 100 = 12. Se pare a fi simplu, dar punerea în aplicare a acestui algoritm, o mulțime de detalii inteligent.
Pentru a crea un program demonstrativ, am lansat Visual Studio, a ales șablon și RandomNumbers proiect numit C # Consola de aplicare. În acest program, nu există nici o dependență semnificativă pe .NET Framework, astfel încât se potrivesc orice versiune de Visual Studio.
Fig. 2. Punerea în aplicare a algoritmului Lehmer
O problemă de punere în aplicare pentru a preveni depășire aritmetică. Algoritmul Lehmer folosește un truc algebrică inteligent. Valoarea q este rezultatul m / a (diviziunea întreg), iar valoarea r este egală cu m% o (m mod a).
La inițializarea RNG Lehmer primare (embrionar) Valoarea poate fi orice număr întreg în intervalul [1, int.MaxValue - 1]. Multe dintre RNG nu are nici un argument-constructor care devine data și ora sistemului, îl convertește la un întreg și utilizat ca valoare inițială.
Lehmer RNG este numit în programul principal metoda de demonstrație:
Fiecare apel Metoda Următoarea returnează o valoare în intervalul [0,0, 1,0) - mai mare sau egală cu 0,0 și strict mai mică de 1,0. Template (int) (hi - lo) * Următoarea + lo) returnează un număr întreg în intervalul [lo, hi-1].
Algoritmul Lehmer este foarte eficient, și în scenarii simple aleg de obicei exact. Dar observați că nici unul dintre algoritmul prezentat în această lucrare nu are nivelul de fiabilitate a criptografic și că acestea ar trebui să fie utilizate numai în situații care nu necesită rigoare statică (rigoarea statistică).
Algoritmul Wichmann-Hill
Acest algoritm este datat 1982 ani. Wichmann Hill Ideea este de a genera trei rezultate preliminare și apoi combinarea lor într-un singur rezultat final. Codul care implementează algoritmul Wichmann-Hill, prezentat în Fig. 3. Codul demo se bazează pe articolul lui BA Wichman (B. A. Wichmann) și A. J. Hill (I. D. Hill) «Algoritmul AS 183: un mod eficient și portabil Pseudo Generator de numere aleatoare».
Fig. 3. Punerea în aplicare a algoritmului Wichmann-Hill
Deoarece algoritmul de Wichmann Hill utilizează trei ecuații generatoare diferite, este nevoie de trei valori inițiale. În acest algoritm, cele trei m-valorile sunt 30269, 30307 și 30323, deci ai nevoie de trei valori inițiale în intervalul [1, 30000]. Ai putea scrie un constructor care ia aceste trei valori, dar apoi v-ar obține o interfață câteva software-ul enervant. Demonstratia utilizat cu o singură valoare inițială parametru care generează trei embrioni de lucru.
Call RNG Wichmann-Hill a purtat același model ca și alte RNG demonstrație:
Wichmann-Hill algoritm este doar puțin mai dificil de implementat decât Lehmer algoritm. Avantajul dintâi în a doua, în care algoritmul Wichmann Hill generează o secvență mai lungă (mai mult de 6 000 000 000 000 valori) înainte de a începe să se repete.
Liniar algoritm congruente
Se pare, și Lehmer algoritm, iar algoritmul Wichmann-Hill pot fi considerate ca fiind cazuri speciale ale așa-numitului algoritm congruential liniar (congruential liniar, LC). Exprimată ca o ecuație, LC este după cum urmează:
Acest lucru corespunde exact Lehmer algoritmul adăugând mai constantă c. Activarea c oferă universal LC-algoritm de proprietăți statistice puțin mai bun decât Lehmer algoritm. implementarea Demonstrație LC-algoritm este prezentat în Fig. 4. Codul se bazează pe standardul POSIX (Portable Operating System Interface).
Fig. 4. Implementarea unui algoritm congruential liniar
LC-algoritm utilizează un număr de operații de biți. Aici ideea este că în tipurile matematice de bază nu funcționează cu tip întreg (32 de biți), și un număr întreg lung (64 de biți). La capătul 32 al acestor biți (de la 16 la 47th inclusiv) sunt extrase și convertite la un întreg. Această abordare dă rezultate mai bune decât folosind un 32 de biți mai tineri sau mai în vârstă, dar din cauza unor complicații de codificare.
Demonstrația a fost un generator de numere aleatoare așa-numitul LC:
Codul anterior Demonstrația utilizează numere aleatoare X (i-7) și X (i-10) pentru a genera următorul număr aleatoriu. Literatura de cercetare cu privire la acest subiect valori (7, 10), sunt denumite în mod obișnuit (j, k). Există alte perechi (j, k), care poate fi utilizat pentru întârzierile algoritmul lui Fibonacci. Mai multe valori recomandate într-o carte bine-cunoscut «Arta de calculator de programare» (Addison-Wesley, 1968) - (24.55) (38.89) (37.100) (30.127) (83.258) (107.378) .
Pentru a inițializa (j, k) în RNG lui Fibonacci cu întârzieri, trebuie să completați mai întâi într-o listă de valori ale k. Acest lucru se poate face în mai multe moduri. Cu toate acestea, cea mai mică dintre valorile inițiale ale lui k trebuie să fie impar. Demonstrația a folosit o metoda brută de copiere valori ale parametrilor de semințe pentru toate valorile inițiale ale lui k, urmată de îndepărtarea primelor valori de 1000 generate. Dacă valoarea semințelor parametru este chiar, atunci prima valoare a lui k este egală cu 11 (număr impar arbitrar).
Pentru a preveni overflow aritmetice, metoda de tip Următorul folosește lung pentru calcule și proprietăți matematice: (a + b) mod n = [(a n mod) + (b mod n)] mod n.
concluzie
Îmi exprim recunoștința pentru revizuirea Microsoft pentru a deveni un expert Chris Lee (Chris Lee) și Oliniku Kirk (Kirk Olynyk).