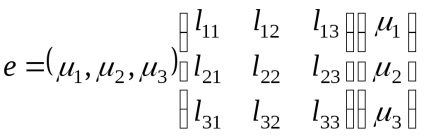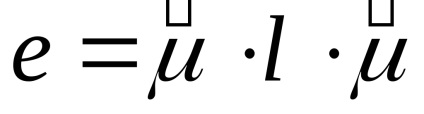Sub deformații mici înseamnă mișcarea unui mediu continuu în care aceasta este o alungire a fibrelor și unghiurile originale cositul relative între fibrele mult mai puțin decât o lungime de fibră fizică și unghiurile dintre ele este mică schimbare. În plus, avem nevoie de componente de deplasare parțiale puțin în raport cu unitatea. În acest caz, în expresiile pentru componentele produsului tensorul c și E L cantități mici pot fi ignorate. Astfel, linearizat deformare tensoriale deformațiile ilitenzory mici sunt de forma:
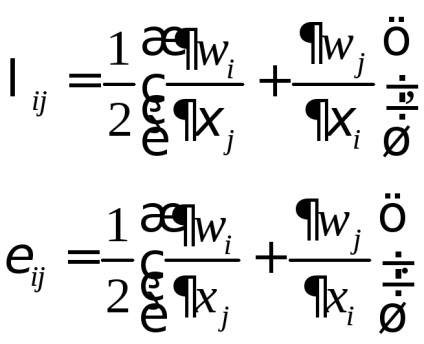
Putem dovedi că tensorul deformațiilor mici la fel.
Exemplu. Să mișcării unui mediu continuu conform legii:
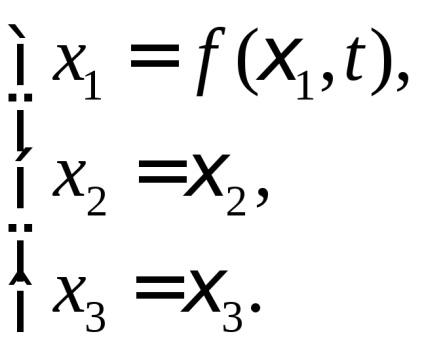
Găsim tensorul L. Pentru aceasta, mai întâi se calculează componentele vectorului de deplasare în coordonatele Lagrangianului:
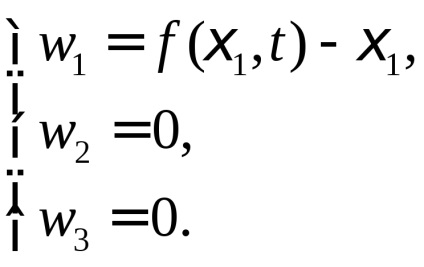
Dintre toate componentele L nenulă ale tensorului va fi doar un singur -
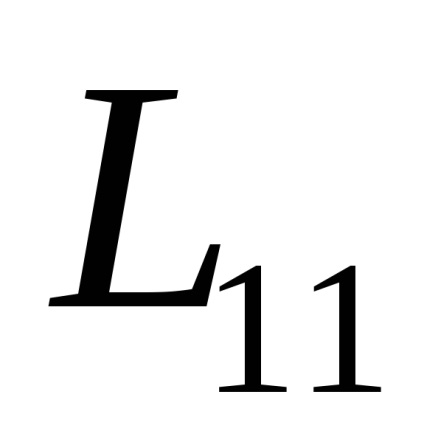
.
Găsim tensor E. În primul rând se calculează componentele vectorului de deplasare în Eulerian coordonate:
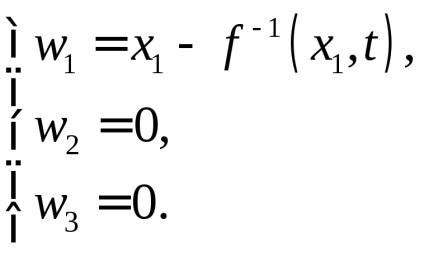
Tensor E are un singur component nenul:
.
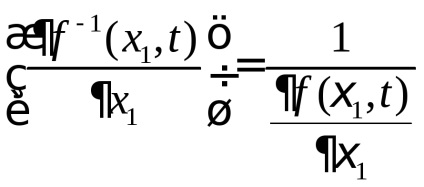
Prin urmare, este ușor de găsit
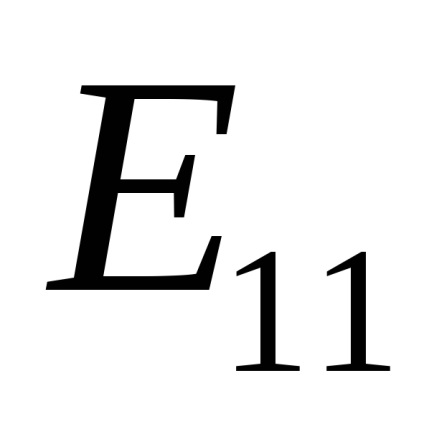
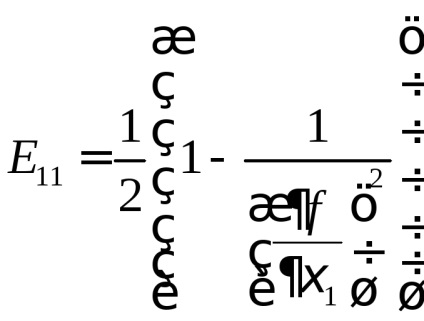
Este evident că
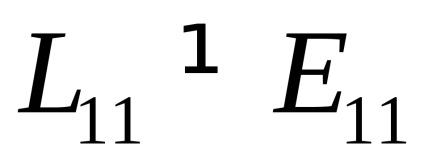
Am găsit tensorul Lagrangiana și Euler deformațiilor mici și arată că acestea sunt aceleași.
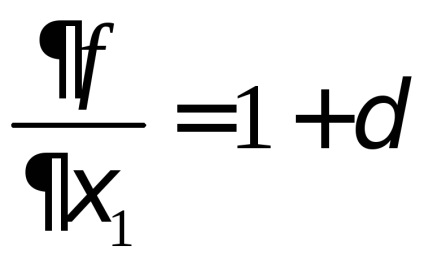
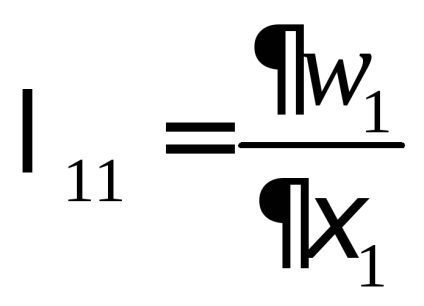

calculăm

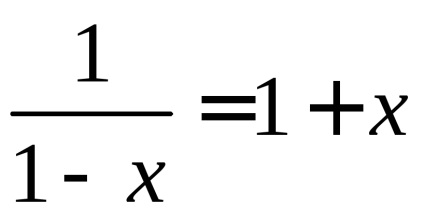
Să calculăm acum relativă lungimea elementului material de schimbare la tulpini mici:
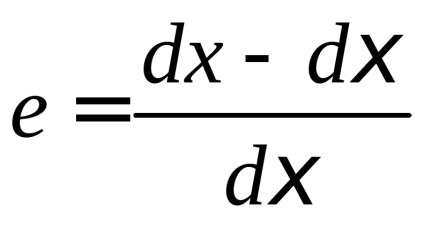
Rezultă că
.
Datorită micimea modificarea relativă a lungimii de deformare este mică, prin urmare, poate fi neglijată în apropierea liniară a pătratul acestei valori:
.
.
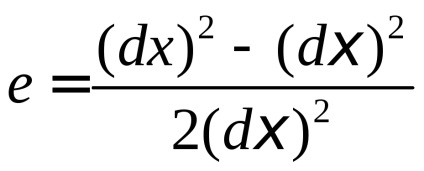
Modificarea relativă în lungime a segmentului exprimat în termeni de tensorului Lagrange sau Euler deformatiilor mici, obținem:
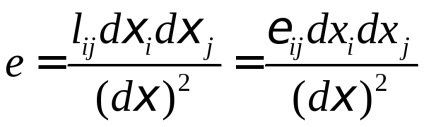
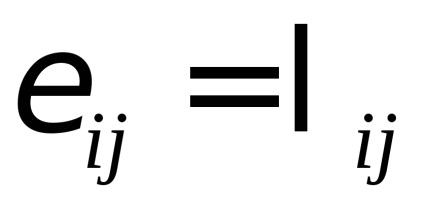
Puteți introduce un vector unitate
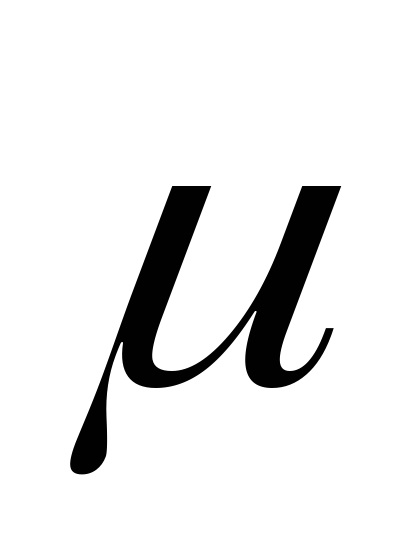
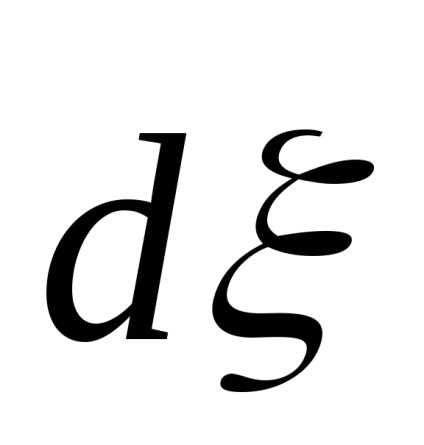
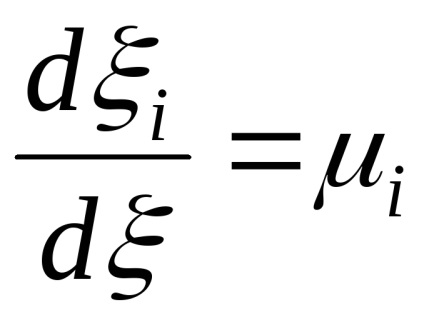
Apoi formula