Foarte multe dintre aceste probleme sunt rezolvate prin construirea suplimentare (Tuning-in, Atașat.). Trebuie să luăm un altul exact aceeași prismă, „a pus“ cu originalul. Punctul superior al prismei adăugat notate cu aceleași litere cu indexul 2, și anume A2, B2 și C2. Este imediat evident că planul dorit (AKS) face parte planul AV2S al triunghiului, și că punctul P se află în mijlocul a1b1.
Mai mult, distanța BH este cea mai simplă de a determina prin piramida de volum AVSV2. Dacă privit ca un plan de baza piramidei triunghiului ABC (înălțime BB2 = 6), volumul
Pe de altă parte, plan ca baza piramidei poate fi considerată AV2S triunghi, în timp ce VN - înălțimea piramidei. Rămâne să se calculeze aria unui triunghi AV2S. El isoscel. Părțile AB2 și CB2 sunt ușor de calculat de Pitagora și √40 egale. Inaltimea, de asemenea, Pitagora este √39. Deci, zona AV2S a triunghiului este (1/2) * 2 * √39 = √39. Apoi HV = 6√3 / √39) = 6 / √13 = 1,664100589
Uita pentru un moment prisma. Există două baze de planuri paralele. Ele se intersectează de-al treilea (aPKC). Liniile de intersecție cu planurile de referință sunt paralele între ele. AS || PK || A1C1, aici laturile bazei superioare și a1b1 S1V1 împărțit în proporții egale, la fel ca în celălalt și înălțimea triunghiului. Prin urmare, punctul „P“ este construit corect.
Astfel de probleme sunt cel mai convenabil rezolvate în stilul geometriei descriptive. În cazul în care desenul se face cu perspectiva corectă. În acest caz, având în vedere vorbitorul final segment, astfel încât să se afișeze planul BNN1B1 al figurii în mărime completă. Dar astăzi dispensa izometrie.
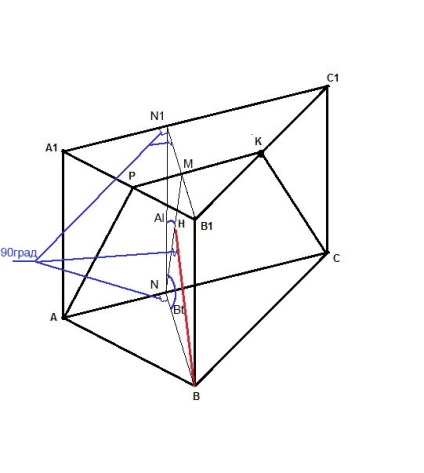
Cea mai mică distanță față de planul perpendicular mănânce, și, prin urmare, BH este perpendicular pe orice linie dreaptă situată în planul, cum ar fi NM.
Noi spunem că partea triunghiul „o“
Înălțimea „h“
înălțimea prismei a „G“
Ceea ce este caracteristic, că creșterea valorii G nu afectează rezultatul calculului. Și în viitor, BH se străduiesc să „h“.