
Sarcina 175. Găsiți raportul dintre două numere complexe, date în formă trigonometrice.
Decizie. Pentru a împărți un număr complex de altul, ai nevoie de un modul de numărătorul împărțit la numitorul unității și numărătorul argumentului scade argumentul numitor. Și, la fel ca și în multiplicarea, trebuie să se asigure că atât numărătorul și numitorul sunt scrise în formă trigonometrice.
Exemplu. Găsiți un număr privat și scrie-l în forma trigonometric:
3 = (cos 11 π + i sin 11 π),
ceea ce implică teorema.
Teorema poate fi formulată cu alte cuvinte, (adică un modul geometric al diferenței dintre cele două numere complexe): modulul diferenței dintre cele două numere complexe este distanța dintre punctele în planul complex, identificat cu aceste numere.
Exemplu. Găsiți triunghi manual format de punctele din planul complex, identificat cu numere complexe: z 1 = 2 + 3i, z 2 = - i, z = 3 - 2.
Decizie. | z 1 - z 2 | = | 2 + 4i | = 2 | 1 + 2i | = 2 5. | z 1 - z 3 | = | 4 + 3i | = 5. | z 2 - z 3 | = | 2 - I | = 5. Răspuns: 5, 5, 2 5.
Sarcina 178. Arată toate punctele de pe planul complex, la distanta de la un punct dat de o distanță predeterminată.
Să presupunem că un punct fix pe planul complex z = o = x o + iy o număr real și a> 0. Necesită
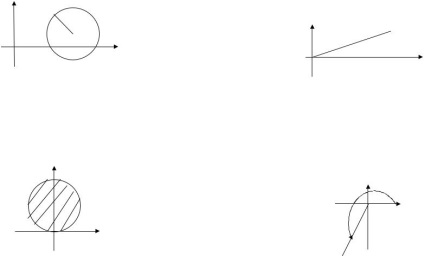
găsi locul geometric al punctelor de acest plan, care îndeplinește condițiile:
a) | z - z O | = A; b) | z - z O | a.
Decizie. Soluția la această problemă este urmată imediat de sensul geometric modulyaraznosti dvuhkompleksnyhchisel. a) Acesta este un punct al cercului de rază centrată la z o.
Capitolul 22. Rădăcinile numerelor complexe
Sarcina 182. Se calculează rădăcina pătrată a unui număr complex.
Definiția. Rădăcina pătrată a numărului complex z este un număr complex α. astfel încât z = α 2.
Din teoria numerelor complexe, se știe că există exact 2 rădăcini zero non-numere complexe, iar ele sunt opuse una față de cealaltă.
Spre deosebire de rădăcini reale aici nu există nici un concept de aritmetică rădăcină pătrată, pentru că nu putem da nici o preferință una dintre cele două rădăcini complexe, astfel încât atât rădăcina unuia desemnat
Să α - una dintre rădăcinile pătrate ale numărului complex z, atunci
Aceasta este, simbolul z este aici mulțimea tuturor rădăcinile pătrate ale numărului complex z. Cu toate acestea, conform tradiției, a scrie
Astfel, rădăcinile sunt situate în mod uniform circumferențial, egal distanțate și împărțiți circumferința în arce n egale. Cu alte cuvinte, punctul de cerc, cu rădăcini de identificare sunt noduri ale unui regulate n-gon.
Definiția. Nodurile de a-n gon se numesc circumferință împărțind puncte (cerc) regulate descris despre un anumit poligon.
Cu alte cuvinte, toate rădăcinile puterii n-lea a numărului complex în planul complex sunt puncte care separă cercul.
Prin urmare, metoda de a găsi rădăcinile tuturor gradul n-lea a numărului complex z = | Z | (Cos φ + i sin φ).
1) n Calculeaza | Z | și este reprezentată în planul complex okruzhnostradiusa n | Z | centrat la origine.
2) Găsiți numărul argument rădăcină 0: arg α o = φ n și izo
mapează grupa a rădăcinii, o punctul corespunzător de pe cerc.
3) Se împarte cercul în n părți egale, folosind faptul că α un punct cyclotomic o avem deja.
4) Se calculează cu formula (2) sau (3), toate argumentele și vom scrie restul rădăcini rădăcini rezultate în înregistrarea formă trigonometrică.
Exemplu. Găsiți toate rădăcinile, în măsura naturală a acestui număr complex și să le reprezinte pe complexul
avion clorhidric: a) 3 i; b) 4 - 1 - i 3. 37