
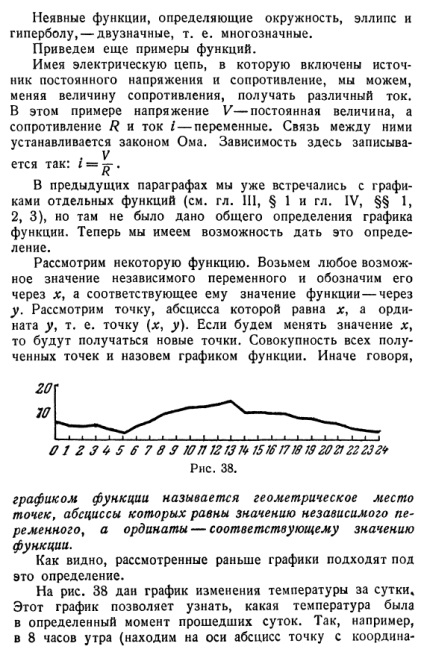



DEFINIȚIE FUNCTII GENERALE § 1. Exemple și definiții Ne-am întâlnit deja cu conceptul unei variabile, variabilă independentă și funcția, dar luate în considerare doar cazurile cele mai simple. Iată câteva exemple de variabile și constante: 1. Cele mai frecvente variabilă - timp. 2. Variabila este temperatura aerului în timpul zilei. 3. Raportul dintre circumferința și diametrul său este constantă - acest număr am. 4. accelerația gravitației este o constantă, dar acest lucru este valabil numai în anumite condiții fizice. 5. ktspeniya constantă chimic pură a temperaturii apei la 100 ° C, dar acest lucru este valabil și la presiune atmosferică normală. Astfel, vom vedea valoarea variabilei, fixe și constantele condiționate. Definiția. Două variabile sunt numite relație funcțională legat, dacă fiecare valoare a unuia dintre ele corespunde uneia sau mai multor alte valori definite. Prima valoare este numită variabila independentă și vtoraya- variabilă dependentă sau funcția. În cazul în care fiecare valoare a variabilei independente corespunde o valoare a funcției, funcția este numită o singură valoare, multi-evaluate între litere altfel. funcție liniară, toate trigonometrice, funcțiile exponențiale și logaritmice sunt amestecate. Funcții implicite care definesc un cerc, o elipsă și o hiperbolă - de două cifre, adică multivalentă ... Noi dau exemple de funcții. Cu un circuit electric care include o tensiune de curent continuu și de rezistență, putem, prin modificarea cantității de rezistență, pentru a primi un curent diferit. În acest exemplu, V constantă tensiunea și rezistența R și actuale / - variabile. Legătura dintre ele este stabilită prin legea lui Ohm. Dependența zapisyva- aici, V etsya acest lucru: În secțiunile anterioare am întâlnit deja cu graficele de funcții individuale (a se vedea capitolul III, § 1 și din capitolul IV, §§ 1, 2, 3 ...), dar nu a fost dat o grafică generală definiție funcție. Acum avem posibilitatea de a da această definiție. Luați în considerare o funcție. Ia orice valoare posibilă a variabilei independente și reprezintă prin x, iar valoarea corespunzătoare a funcției - în ceea ce privește y. Să considerăm punctul a cărui abscisă este jc, iar ordonata y, z. E. Punctul (x, y). Dacă vom schimba valoarea lui x, atunci vom obține noi puncte. Colectarea tuturor punctelor de date și apel grafic al funcției. Cu alte cuvinte, Fig. 38. Graficul funcției este locul geometric al punctelor a căror abscise egală cu valoarea variabilei independente, iar pe ordonată - valoarea corespunzătoare a funcției. După cum se poate observa, grafice anterioare discutate se potrivesc această definiție. Fig. 38 este un grafic al modificărilor de temperatură pe zi * Acest grafic vă permite să știi ce temperatura a fost la un moment dat în ultimele zile. De exemplu, în ora 8 (situat pe abscisă cu punctul de coordonate-8), temperatura a fost de 10 grade Celsius (perpendicular vosstavlenny punctului constatat axa x are o scală gradată în receptate 10 unități de lungime). Astfel, graficul prezentat în Fig. 38, stabilește o corespondență între fiecare punct în timp și numărul dând temperatura la acest punct. Notă. Funcția se numește nu numai variabila dependentă, dar, de asemenea, legea sau o metodă care stabilește corespondența dintre variabilele dependente și independente. De exemplu, dacă o funcție dată y = x 8 + Uh9 se poate spune că funcția dată x * - \ - yi. Există mai multe modalități de funcțiile de locuri de muncă; cele mai multe funcții sunt date de ecuațiile, tabele sau grafice. De exemplu, o funcție liniară dată de ecuația; funcție dând modificarea temperaturii în timpul zilei, orarul de obicei specificat; dependența de unghiul de vedere al distanței este dată de masă. La fel ca și în algebra Lie pentru a indica numerele introduse litere și funcțiile se introduce notația, în general, următoarele. Dacă y este o funcție de, ah, variabila independentă, vom scrie y = / (*). În cazul în care / denotă setul și operații matematice de ordine (adunare, scădere, înmulțire, împărțire, exponentiala, constatare logaritmi constatare trigonometrice, etc ...). Înregistrate despre / între paranteze pus în care scrie pe ceea ce este necesar pentru a produce aceste acțiuni. Scrierea y = f (x) este citită ca: y este o funcție de x. EXEMPLUL 1./(*) = J / V +1. Aici, / reprezintă: 1) Ridicați-a treia putere; 2) se adaugă o unitate; 3) extragerea rădăcinii pătrate. Exemplul 2. y = zf (x) - 2 păcatul jc. Aici, / reprezintă: 1) a găsit valoarea sine; 2) se înmulțește cu doi. Exemplul 3: Y = / (x) = x * + 4n; 2+ 5. Aici, / reprezintă: 1) Ridicați puterea a treia; 2) Ridicați al doilea grad; 3) Rezultatul obținut în paragraful precedent, se înmulțește cu 4; 4) numărul obținut în paragrafele 1 și 3, complexul; 5) a fost adăugat la numărul obținut din cinci anterioare. Exemplul 4. Funcția f (x) este definit după cum urmează: dacă l. apoi / (x) = 0; dacă este 1, atunci / (*) = 1; dacă x> 1, /(.*) = 0. Deși nu este specificat, folosind orice funcții matematice și operații funcție / (x în acest exemplu), exprimate în termeni de x, cu toate acestea, este posibil să se specifice valori pentru orice x. De exemplu, fie x = - 3, în acest caz, inegalitatea -3, deci / (- 3) = 0. Dacă x = - ^ = y = inegalitatea și, prin urmare, = 1. Dacă x = 11,5 atunci inegalitatea 11.5> 1, deci / (11,5) = 0. funcția de acest fel, așa cum tocmai sa arătat, se regăsesc nu numai în manualele de matematică; acestea sunt adesea găsite în fizica și tehnologia modernă. Să considerăm circuitul din Fig. 39. Aici, B semnifică o sursă constantă forță electromotoare (de exemplu, baterie), B-switch, un ampermetru A, R-rezistență. Fig. 40. Fig. 39. În cazul în care comutatorul este deschis, calea actuală nu este prezentă și ampermetru arată 0; dacă vom închide comutatorul, curentul continuu și ampermetru va arăta valoarea ei va apărea în lanț. ac ampermetru va fi fixat tot timpul pentru a opri comutatorul. În cazul în care coordonatele axei orizontale va întârzia ty timp, iar cealaltă axa magnitudinii / curent, graficul relației funcționale va arăta așa cum este prezentat în Fig. 40. În această figură, tx reprezintă punctul de comutare curent, un punct-tt off. Diverse funcții, există un set infinit, astfel încât să nu se poate, și nu au nevoie, fiecare dintre ele pentru a da un anumit nume. Dar, cu toate acestea, anumite funcții de multe ori dau nume. Iată câteva dintre ele: liniare, pătratice, trigonometrice,, funcții exponențiale logaritmică, polinomială de putere (sau un polinom) de forma y = ya0hp + § 2. Regiunea existenței funcției Definiție. Setul de toate valorile variabile independente pentru care legea sau regula care permite pentru a găsi valoarea corespunzătoare a funcției, numit domeniul de existență a funcției. Exemplul 1. Domeniul tehnic al existenței funcției y = X este format din toate numerele reale altele decât zero, deoarece este imposibil să se împartă cu zero. Exemplul 2. Regiunea de existență a funcției y => /
x este format din toate numere întregi non-negative. Numerele negative nu fac parte din domeniul de existență, ca rădăcina pătrată a unui număr negativ este un număr complex, și numere complexe, noi nu facem. Exemplul 3. Funcția y = \ gx are o suprafata fiind de Florii, format din toate numerele pozitive, r. E. X> 0. Exemplul 4. y =
T regiune * a existenței acestei funcții, toate numerele reale, cu excepția -1 și +1. Numerele - 1, și care nu fac parte din domeniul de existență, deoarece numitorul este zero și zero, delnt imposibil pentru aceste valori. j Exemplul 5: y = ^. Regiunea existenței cuprinde toate numere întregi pozitive, cu excepția unităților.