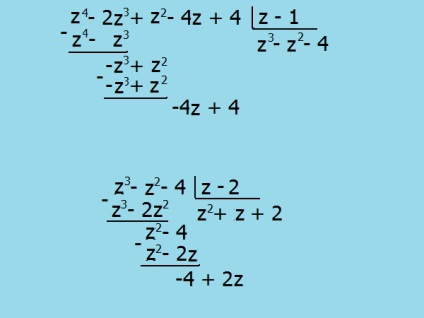Simplificarea expresiilor algebrice este necesară în multe domenii ale matematicii, inclusiv la decizia ecuațiilor de grade mai mari, diferențiere și integrare. Acesta utilizează mai multe metode, inclusiv de factoring. Pentru a aplica această metodă, trebuie să găsiți și să facă un factor comun din paranteze.

Impunerea unui factor comun din parantezele - una dintre cele mai comune modalități de factoring. Această tehnică este utilizată pentru a simplifica structura expresiilor algebrice lungi, adică polinoame. factor comun poate fi un număr, un monom sau binom, precum și pentru a căuta se aplică proprietatea distributiv de multiplicare.
Chislo.Posmotrite atent pe coeficienții pentru fiecare element al unui polinom, putem să le împărți în același număr. 4 va • (3 • z³ + 4 • z² - 1) 4 factor evident este 4. După conversie - de exemplu, în expresie 12 • z³ + 16 • z². Cu alte cuvinte, acest număr este cel mai mic divizor comun întreg al tuturor coeficienților.
Odnochlen.Opredelite includ dacă aceeași variabilă în fiecare dintre termenii din polinomul. Să presupunem că este așa, acum uita-te la factorii la fel ca în cazul precedent. EXEMPLUL 9 • z ^ perioada 4 - 6 • z³ + 15 • z² - 3 • z.
Fiecare element al acestui polinom include o z variabilă. Mai mult, toți coeficienții - multiplilor 3. Prin urmare, un factor comun va monom 3 • z: 3 • z • (3 • z³ - 2 • z² + 5 • z - 1).
paranteze Dvuchlen.Za impus factor comun al celor două elemente, și un număr variabil care este o soluție de polinom comun. Prin urmare, în cazul în care factorul -dvuchlen nu este evident, aveți nevoie pentru a găsi cel puțin o rădăcină. Evidențiați termenul liber al polinomului, un coeficient fără o variabilă. Acum, se aplică metoda de substituție într-o exprimare generală a tuturor divizori integrale ale termenului constant.
Să considerăm un exemplu: z ^ 4 - 2 • z³ + z² - 4 • z + 4. Verificați dacă oricare dintre divizorii întregi de 4 rădăcină a ecuației z ^ 4 - 2 • z³ + z² - 4 • z + 4 = 0. Prin simpla substituire a localiza z1 = z2 = 1 și 2, înseamnă că suporturile pot fi luate binomi (z1) și efortul (z2). Pentru a găsi restul expresiei, utilizați serial divizia lung.