Pentru a utiliza formule de reducere, există două reguli.
1. Dacă unghiul poate fi reprezentat ca (π / 2 ± a) sau (3 * π / 2 ± a), numele funcției este schimbat la păcat cos, cos la păcat, tg pe ctg, ctg la tg. Dacă unghiul poate fi reprezentat ca (π ± a) sau (2 * π ± a), numele funcției rămâne neschimbată.
Uită-te la imaginea de mai jos, este prezentat schematic, atunci când pentru a schimba semnul, și când nu.
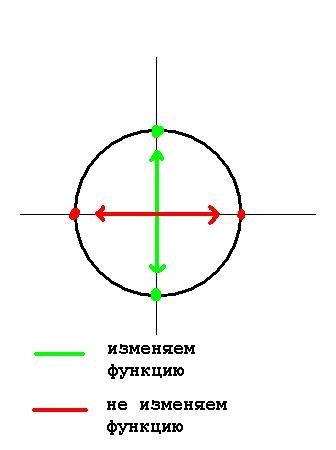
2. Regula „așa cum ai fost, așa că ai rămas.“
Semnul de mai sus funcția rămâne aceeași. Dacă funcția inițială a fost „plus“ semn, atunci funcția de mai sus este „plus“ semn. Dacă funcția inițială a fost „minus“ semn, atunci funcția de mai sus are semnul „minus“.
Diagrama de mai jos prezintă semnele majore ale funcțiilor trigonometrice, în funcție de trimestru.
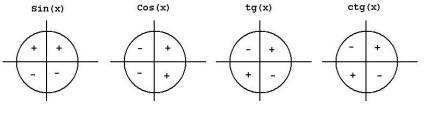
Noi folosim formulele de mai sus:
Păcatul (150˚) se află în al doilea trimestru, Figura vedea că semnul păcatului în acest trimestru este de +. Deci, în funcția de mai sus va fi, de asemenea, „plus“ semn. Acest lucru am folosit a doua regulă.
Acum 150˚ = 90˚ + 60˚. 90˚ este tt / 2. Aceasta se ocupă cu cazul π / 2 + 60, astfel încât prima schimbare regula funcție păcat cos. Ca rezultat, vom obține Sin (150˚) = cos (60) = ½.
Dacă se dorește, aducând toate formulele pot fi reduse la o singură masă. Dar este mai ușor să ne amintim aceste două reguli și de a le folosi.