Viteza și accelerația
Fie funcția \ (s \ stânga (t \ dreapta) \) descrie poziția unui obiect într-un sistem de coordonate la momentul \ (t \). Apoi, prima derivată a funcției \ (s \ stânga (t \ dreapta) \) este viteza instantanee a obiectului:
\ (V = s ^ = f „\)
Derivata a doua a funcției \ (s \ stânga (t \ dreapta) \) reprezintă accelerația instantanee a obiectului:
\ (W = v ^ = s ^ = f '' \)
Ecuația tangentei
\ (Y - = f ^ \ prime \ dreapta)> \ dreapta)> \)
unde \ (\ stânga (\ dreapta) \) - coordonatele punctului de atingere, \ (f ^ \ prime \ dreapta)> \) - valoarea funcției derivate \ (f \ left (x \ dreapta) \), la punctul de tangență.
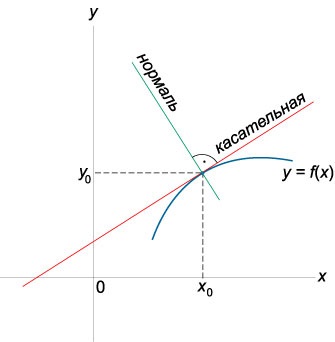
unde \ (\ stânga (\ dreapta) \) - coordonatele punctului în care a efectuat normal \ (f ^ \ prime \ dreapta)> \) - valoarea funcției derivate \ (f \ stânga (x \ dreapta) \) în acest punct.
Creșterea și scăderea funcției
Dacă \ (f „\ stânga (> \ dreapta)> 0 \), apoi crește funcția de la punctul \ (\). Figura de mai jos este o funcție crescătoare cu \ (x \).
Dacă \ (f '\ stânga (> \ dreapta) 0 \)) pentru toate \ (x \) într-un anumit interval \ (\ stânga (> \ right] \) și scade (\ (f' \ stânga (x \ dreapta ) 0 \)) pentru toate \ (x \) în intervalul \ (\ stânga [, b> \ dreapta) \), atunci funcția \ (f \ stânga (x \ dreapta) \) are un minim local la punctul \ (\ ).
Al doilea un criteriu suficient pentru existența extremum
Dacă \ (f '\ stânga (> \ dreapta) = 0 \) și \ (f' „\ stânga (> \ dreapta) 0 \), atunci funcția \ (f \ left (x \ dreapta) \) are un minim local la punctul \ (\).
funcţii convexe
Funcția \ (f \ stânga (x \ dreapta) \) este concavă (sau concavă) la punctul \ (\) în cazul în care derivatul \ (f „\ stânga (x \ dreapta) \) la care scade punctuale (decalaj \ ( x \)).
condiții suficiente pentru convexitate sus și în jos
Dacă \ (f '' \ stânga (> \ dreapta)> 0 \), atunci funcția \ (f \ left (x \ dreapta) \) este convexă în jos, la punctul \ (\).
Dacă \ (f '' \ stânga (> \ dreapta)