Mutarea de-a lungul marginilor G (X, U), puteți trece de la vârful la vârful. Orice secvență de muchii obținute în același timp, se numește rută. adică secvența (x0, x1) (x1, x2) ... (xn, xn-1), în care oricare două nervuri adiacente adiacente - traseu.
Chain - un traseu care toate marginile sunt distincte.
lanț simplu - lanț în care toate nodurile sunt diferite.
Ciclul - lanț în care același început și de sfârșit nodurile.
Arbore - conectat grafic fără cicluri. În copac, oricare două noduri sunt conectate printr-un singur lanț. Arborele construit pe n noduri are n-1 muchii.
Lemn - un set de copaci.
Graficele sunt două cicluri minunate: Euler și Hamiltonian.
Contele nazyvaetsyaeylerovym. în cazul în care pentru fiecare vârf al graficului este traseul începe și se termină la vârful și trece prin fiecare muchie doar o singură dată. Un astfel de traseu se numește ciclu Euler.
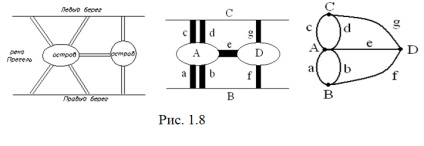
Problema a apărut din exemplul următor. În secolul al XIII-lea, locuitorii din Königsberg, pe jos peste poduri râu Pregelul a încercat să rezolve problema: (. Figura 1.8) Este posibil pentru a obține în jurul valorii de toate podurile, trecând pe fiecare dintre ele doar o singură dată
Sarcina este după cum urmează. să efectueze o plimbare în jurul orașului, astfel încât, după ce trece exact o dată pe fiecare punte de legătură pentru a reveni la același loc de unde a început plimbare. Rezolvarea acestei probleme, Euler Konigsberg descris ca un grafic, identificând-o cu părțile superioare ale orașului, și marginile - cu poduri, care sunt asociate cu aceste părți.
Euler a reușit să demonstreze că traseul dorit ocolind orașul nu există.
Răspunsul poate fi obținut pe baza următoarei teoremă.
Teorema. Un grafic este Eulerian dacă și numai dacă gradele de toate nodurile sale sunt chiar.
După cum se poate observa din figură, simulatorul de circuit poduri count, toate nodurile au grad impar. Prin urmare, ciclul Euler în acest grafic nu există.
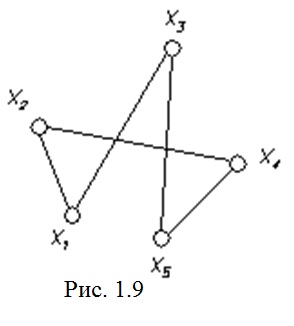
EXEMPLU grafic având ciclu Eulerian este prezentat în Fig. 1.9.
Un grafic este hamiltonian. dacă (toate marginile nu pot participa în acest caz) se începe ruta și se termină în partea de sus și trece prin toate nodurile doar o singură dată pentru fiecare nod al graficului. Acest traseu se numește ciclu hamiltonian.
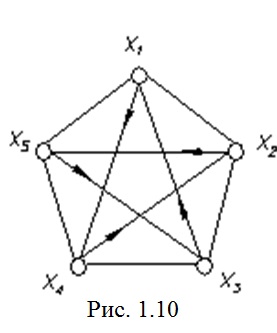
Graficul complet cu numărul de noduri n »2 există întotdeauna un ciclu hamiltonian. Un exemplu de un astfel de ciclu este prezentată în Fig. 1.10 - (x1, x4) (x4, x2) (x2, x5) (x5, x3) (x3, x1).
Graficele hamiltoniene sunt utilizate pentru modelarea multe probleme practice, de exemplu, să servească drept model în pregătirea orarelor. Baza tuturor acestor probleme este o problemă clasică de călătorie agent de vânzări: vânzătorul trebuie să tur al orașului și înapoi, vizitând fiecare oraș exact o dată, la reducerea costurilor de transport la un nivel minim, în același timp.
Modelul grafic al problemei comis-voiajorului este un grafic Hamiltonian, ale cărui noduri reprezintă orașul, iar marginile - conectarea acestora la drum. Mai mult, fiecare nervură este echipată cu o greutate care indică costuri de transport necesare pentru a călători modul corespunzător, cum ar fi, de exemplu, distanța dintre orașe, sau deplasarea pe drum. Pentru a rezolva problema, este necesar să se găsească un ciclu hamiltonian de greutate totală minimă.