Ecuația tangentei în coordonate carteziene
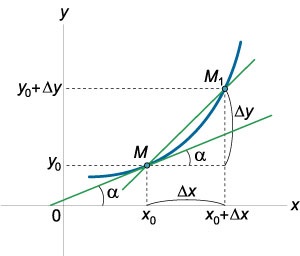
Presupunem că funcția \ (y = f \ stânga (x \ dreapta) \) este definit pe intervalul \ (\ stânga (\ dreapta) \) și continuă în punctul \ (\ în \ stânga (\ dreapta). \) În litera (punctul \ (M \) în figura \ (1 \)) are valoarea \ (= f \ stânga (> \ dreapta). \)
Să variabila independentă la punctul \ (\) este incrementată cu \ (. \ Delta x \) Creșterea corespunzătoare a funcției \ (\ Delta y \) este dat \ [\ Delta y = f \ stânga (+ \ Delta x> \ dreapta) - f \ stânga (> \ dreapta). \] Figura \ (1 \) litera \ (\) are coordonatele \ (\ stânga (+ \ Delta x, + \ Delta y> \ dreapta). \) construi \ secant ( M. \) ecuaţia lui este de forma \ [y - = k \ left (> \ dreapta) \] unde \ (k \) - coeficientul unghiular în funcție de increment \ (\ Delta x \) și egal \ [k = k \ stânga (\ dreapta) = \ frac >> \] Când reducerea \ (\ Delta x \) punctul \ (\) tinde la punctul \. (M: \) \ (\ M. \) În limita \ ( \ Delta x \ la 0 \), distanța dintre punctele \ (M \) și \ (\) tinde la zero. Acest lucru rezultă din funcția continuitate \ (f \ stânga (x \ dreapta) \) la punctul \ (: \) \ [\ Delta y = 0,> \; \; \ Stânga |> \ dreapta |> = \ sqrt \ dreapta)> ^ 2> + \ dreapta)> ^ 2 = 0. >>> \] Poziția de limitare a secantă \ (M \) reprezintă doar linia tangentă la graficul funcţia \ (y = f \ left (x \ dreapta) \) la punctul \ (M. \)
Există două tipuri de tangentelor - înclinate și verticale.
Definiție \ (1 \).
Dacă există o limită \ finită (\ lim \ limits_ k \ stânga (\ dreapta) =, \), atunci linia dreaptă având ecuația \ [y - = k \ stânga (> \ dreapta) \] numita tangent inclinata la graficul de \ ( y = f \ stânga (x \ dreapta) \) la punctul \ (\ stânga (,> \ dreapta). \)
Definiția 2.
Dacă valoarea limită \ (k \) când \ (\ Delta x \ la 0 \) este infinit: \ (\ lim \ limits_ k \ left (\ dreapta) = \ pm \ infty, \), atunci linia dreaptă având ecuația \ [ x =, \] se numește tangenta verticală la graficul de \ (y = f \ left (x \ dreapta) \) la punctul \ (\ stânga (,> \ dreapta). \)
Foarte important, \ [= \ lim \ limits_ k \ left (\ dreapta)> = \ frac >>> => \ dreapta),> \] adică panta liniei tangente egală cu valoarea funcției derivate \ (f \ left (> . \ dreapta) \), la punctul de tangență \ (\) prin urmare, tangenta ecuație înclinată poate fi scrisă sub forma: \ [= f „\ stânga (> \ dreapta) \ stânga (> \ dreapta) \; \; \ textul> \ ; \ ;.> \ dreapta) \ stânga (> \ dreapta) + f \ left (> \ dreapta)> \] deoarece panta liniei este egală cu panta \ (\ alpha, \) ce linie face cu direcția pozitivă a axei x , atunci următoarea ecuație ternar: \ [. k = \ tan \ alpha = f „\ stânga (> \ dreapta) \]
Ecuația normală în coordonate carteziene
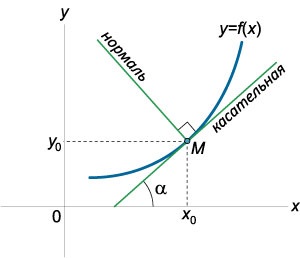
O linie dreaptă perpendicular pe tangenta și care trece prin punctul de contact \ (\ stânga (,> \ dreapta), \) este numit normal la graficul \ (y = f \ stânga (x \ dreapta) \), în acest punct (Figura \ (2 \ )).
Din geometria cunoscut că produsul coeficienților unghiulare ale liniilor este perpendicular \ (- 1 \) Prin urmare, cunoscând ecuația tangentei la punctul \ (\ stânga (,> \ dreapta): \) \ [y - = f „\ stânga (> \ dreapta) \ stânga (> \ dreapta), \] putem scrie imediat în jos ecuația normal în forma \ [y - = -. \ frac> \ dreapta) >> \ stânga (> \ dreapta) \]
Ecuațiile tangentă și normală în formă parametrică
Tangentă și ecuații normale, în coordonate polare,
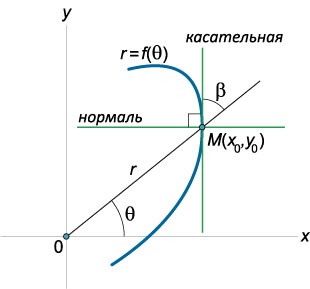
Să presupunem că curba este dată polară ecuația \ (r = f \ stânga (\ theta \ dreapta), \) care exprimă dependența lungimii vectorului rază \ (r \) al unghiului polar \ (\ theta. \) În coordonate carteziene, o curbă va fi descris de un sistem de ecuații \ [\ left \<\begin x = r\cos \theta = f\left( \theta \right)\cos \theta \\ y = r\sin \theta = f\left( \theta \right)\sin\theta \end \right..\] Таким образом, мы записали уравнение кривой в параметрической форме, где роль параметра играет угол \(\theta.\) Далее легко получить выражение для углового коэффициента касательной, проведенной к кривой в точке \(\left( ,> \ Dreapta): \) \ [>>>>> = \ dreapta)> ^ \ prim >>> \ dreapta)> ^ \ prim >>>> = \ păcat \ theta + r \ cos \ theta >> \ cos . \ theta - r \ păcat \ theta >>> \] Ca rezultat, ecuația tangentă și normală va fi scrisă sub forma: \ [= \ frac >>>> \ stânga (> \ dreapta)> \; \; \; ),> \] \ [= - \ frac >>>> \ stânga (> \ dreapta)> \; \; \; ).> \] Studiul curbei poate fi realizată direct în coordonate polare, fără trecerea la un sistem cartezian. În acest caz, unghiul de înclinare tangentă care este determinată nu \ (\ theta \) cu axa polară (adică direcția pozitivă a direcției axei x), și unghiul \ (\ beta \) la linia care conține vectorul raza \ (r \) (Figura \ (3 \)).
Parabolei definită de ecuația \ (y = + 2x + 3. \) Creare ecuație tangent la parabolei, care trece prin punctul \ (A \ stânga ( <- 1,1> \ Dreapta). \)
Transforma ecuația parabolei să însemne \ [+ 2x + 3> = + 2x + 1 + 2> = \ dreapta) ^ 2> + 2> \] Se poate observa că graficul parabolei se obține din graficul funcției \ (y = \) în rezultatul transportului paralel \ (1 \) și una la stânga pe \ unitate (2 \) în sus (Figura \ (7 \)).
Găsim ecuația a doua tangente la parabolei, care trece prin punctul \ (A \ stânga ( <- 1,1> . \ Dreapta) \) Fiecare dintre aceste tangentelor definite de ecuația \ [= k \ stânga (> \ dreapta),> \; \; \ Dreapta)> \ dreapta),> \; \; \; \; \] Unde \ (k \) - panta (\ (\) - pentru prima tangenta \ (\) - pentru al doilea).
Astfel, problema se reduce la determinarea pantei tangent \ (\) și \ (. \) Se consideră că punctele de tangență \ (B \) și \ (C \) condiție \ [y = kx + k + 1 \\ y = + 2x + 3 \ end \ drept,> \ ;. \; + 2x + 3.> \] Mai mult decât atât, la punctele de tangență \ (B \) și \ (C \) este valoarea pantei funcției derivat \ (y = + 2x + 3 \) Deoarece \ [+ 2x + 3> \ dreapta) ^ \ prim >> = \] apoi, în consecință, obținem o altă ecuație în forma \ [k = 2x + 2. \] Ca rezultat, avem un sistem de două ecuații \ [\ left \<\begin kx + k + 1 = + 2x + 3\\ k = 2x + 2 \end \right.\] с двумя неизвестными \(k\) и \(x.\) Решая эту систему, находим значения \(k\) и \(x\) (т.е. угловые коэффициенты касательных \(,\) \(\) и абсциссы точек касания \(B\) и \(C\)): \[ kx + k + 1 = + 2x + 3\\ k = 2x + 2 \end \right.,>\; \; \ Dreapta) x + 2x + 2 + 1 = + 2x + 3> \; \; + 2x + 2x + 3 = + 2x + 3> \; \; + 2x = 0,> \; \; = - 2 \; = 0.> \] prima decizie \ (= - 2 \) corespunde punctului \ (B. \) a doua soluție \ (= 0 \) este coordonata punctului tactil \ (C. \) Coeficienții unghiulare au următoarele valori:-
tangentă \ (AB: \; \) \ (y = -2x - 1; \)
tangentă \ (AC: \; \) \ (y = 2x + 3 \)
La un grafic al \ (y = \ cos x \) a avut loc tangent la punctul \ (M \ stânga (,> \ dreapta), \) unde \ (0 0, doar un singur \] derivatul are punctul critic, care este determinată de starea de \ [z = 0,> \; \; \ dreapta) = 0,> \; \; \] Această ecuație poate fi rezolvată numeric. Cu toate acestea, se poate observa că, dacă \ (z = \ mare \ frac \ normalsize, \), atunci partea stângă a ecuației este negativ: \ [:> \; \; - \ cot \ frac> = - 1 \ aprox - 0,21 0.> \] Prin urmare, punctul extremum al funcției \ (S \ stânga (z \ dreapta) \) este cuprins în intervalul unghiului \ (\ stânga (\ normalsize, \ mare \ frac \ normalsize> \ dreapta) \) (Figura \ (12 \)), iar acest punct este un punct minim (în funcție de natura modificărilor derivate semn).
Coordonatele aproximative ale punctului minim poate fi calculat, de exemplu, în Excel. Este vorba \ (0,86 \; \ textul \) (. 49.3 ^ \) sau \

articole similare