Secțiunea II. stereometrie
1. Definiția cutiei, proprietățile sale.
Este o cutie numită o prismă, care este baza de paralelogramului.
În toate aspectele cutiei - paralelogram.
Din moment ce o cutie este o prismă, toate proprietățile prismei sunt de asemenea valabile pentru caseta.
Paralelipiped ale cărei margini laterale sunt perpendiculare pe planul de masă, numit un paralelipiped drept. partea lui se confruntă cu - dreptunghiuri. În Figura 459 prezintă un drept paralelipipedic.
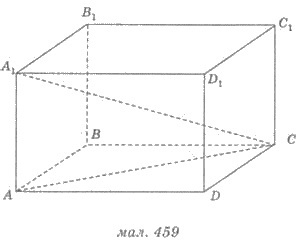
Dacă marginile laterale ale paralelipipedului nu sunt perpendiculare pe planul de bază, numit paralelipiped oblic. In Figura 460 prezintă un paralelipiped înclinat.
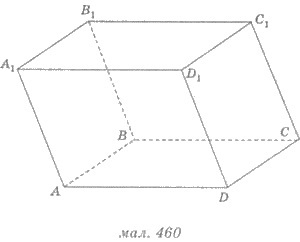
Face din cutie, fără noduri comune, numite fețele opuse. Figura 460 fețele opuse sunt fețele ABC D și A 1 B 1 C 1 D 1. AVV1 A1 și C 1 C 1. DD AA 1 D 1 D 1 C BB1 și S.
Luați în considerare caseta de proprietăți.
1) paralelă cu fețele opuse ale paralelipipedului și egal.
2) diagonalele paralelipipedului și punctul de intersecție de intersecție sunt secționate.
EXEMPLUL 1 părți directe de bază paralelipipedice sunt de 10 cm și 17 cm, iar una dintre diagonalelor bazei de 21 cm. O mare diagonală a paralelipipedului este egală cu 29 cm. Găsiți aria suprafeței laterale a paralelipipedului.
Soluții. 1) Fie a = 10 cm și b = 17 cm - parte a bazei; d 1 = 21 cm - fundație diagonală. Conform proprietății diagonalelor cutiei: aici
Deoarece 21, diagonala cea mai mare a paralelipipedului care este o proiecție pe planul de bază este diagonala bazei cu lungimea de 21 cm.
. 2) (Fig 459) AC = 21 cm; A 1 P = 29 cm.
3) Deoarece paralelipipedul dreapta este o vedere a unei prisme drepte, zona S bici suprafață laterală dreapta paralelipipedic poate fi găsit prin formula S = bici Pl, unde P - perimetrul bazei, l - lungimea marginilor laterale.
T = 2 (10 + 17) = 54 (cm). S = 54 bici ∙ 20 = 1080 (cm 2).
Exemplul 2. Baza este un drept paralelipiped cu latura romburi 4 cm și un unghi ascuțit de 60 °. Este mai mic caseta este egal cu diagonala diagonalei lungi a rombului. Găsiți volumul cutiei.
Soluții. 1) Fie D ABC A1 B1 C1 D 1 - specificată într-o stare paralelipipedica; ABC D - romburi; AC = 4 cm; B AD = 60 ° (Fig. 461).
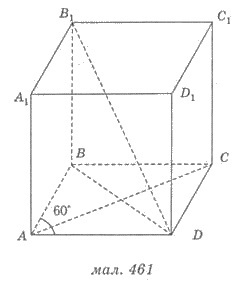
2) o suprafață de bază
3) Δ AVB - echilateral; AB = BD = 4 cm.
4) Δ ABC ABC = 90 °. prin teorema cosinusului:
5) De la AC D, B 1 D - mai mici diagonal al paralelipipedului.