Necesitatea de a introduce determinant - numărul care caracterizează o matrice A pătrat, -tesno legat la soluția de ecuații liniare. Determinantul A este notat | A |
Determinantul matricei A = comanda primului A11. sau determinant al primului ordin, se numește a11 elementul. Δ1 = | A | = a11
De exemplu, să A = (3), apoi Δ1 = | A | = 3
Determinantul matricei de ordinul doi A = (aij) sau un determinant al doilea ordin, este numărul care se calculează cu formula:
Determinant treia matrice comanda A = (aij) sau al treilea ordin, este numărul care se calculează cu formula:

La calcularea determinantului celei de a treia metodă, pentru utilizarea Sarryusa. Noi scrie toate elementele determinant și atribuie dreptul de primele două coloane ale determinantului:
Ia semnul „+“ produs al elementelor de pe diagonala principală și cele două linii paralele (adică, să ia semnul produsului, fără a schimba) și cu semnul „-“ produs al elementelor diagonale secundare și două linii paralele cu ea (adică semn al produsului de elemente inversat). Luând suma algebrică, obținem determinant al treilea ordin.
Problema 1. Calculați determinant al treilea ordin:
Proprietățile determinanților
- Schimbul de două coloane sau două rânduri de determinant este echivalentă cu înmulțirea cu -1.
- Dacă determinantul are două coloane identice sau două rânduri de identic, este egal cu zero.
- Multiplicarea tuturor elementelor unei singure coloane sau a unui rând de determinant pe orice lambda număr este echivalent cu multiplicarea determinant prin acest număr λ.
- Dacă toate elementele unei coloane sau a unui rând de determinantul este zero, atunci determinantul este zero în sine.
- nu se schimbă atunci când determinantul matricei transpune, adică | .. A | = | A T |
- În cazul în care elementele celor două coloane sau două rânduri ale determinantului proporțional, determinantul este zero.
- În cazul în care elementele unei coloane (rand) determinantului adaugam elementele corespunzătoare din altă coloană (linia) înmulțită cu orice lambda factor comun, valoarea determinantului nu se schimbă.
Urmatorul factor determinant al proprietății legate de conceptele și completările minore algebrice. Minor Element M ij a ij a matricei A = (a ij) (i, j = 1,2, ..., n) n-lea ordin se numește determinantul (n-1) comanda -lea, matricea rezultată A cu anularea i-lea rând și coloana j-lea. De exemplu, un element minor 32 al treilea ordin este determinantul matricei de ordinul doi:
Cofactor Aij elementul aij al matricei A ordinul n-lea este numit minor sa luat cu semnul (-1) 1+ j.
8. (Laplace Teorema) determinant este suma produselor elementelor din orice coloană (rând) prin cofactori lor, adică dacă A = (aij), atunci:
(Descompunere elementelor i-lea rând; i = 1,2,3, ..., n);
(Descompunere elementele coloanei j-a;. J = 1,2, ..., n).
Problema 2. Se calculează determinantul matricei:
Alegeți o coloană (sau rând), care conține cele mai multe zerouri, de exemplu, prima linie și extinde-l pentru a determinantului cu ajutorul determinant proprietății 8. obține un al treilea ordin. De asemenea, constată că prin 8 proprietăți de descompunere, cum ar fi a treia coloană:

In determinant matrice ychislenie în MS Excel
Pentru a calcula determinantul matricei formează foaia MS Excel:
- Definim matricea inițială.
- Definim un loc în rezultat.
- Referindu-se la funcțiile de bază, vom găsi MDETERM funcția. efectua formularea problemei.
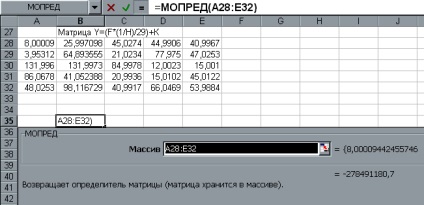
Pentru a finaliza munca în timp ce apăsați Shift / Ctrl / Enter
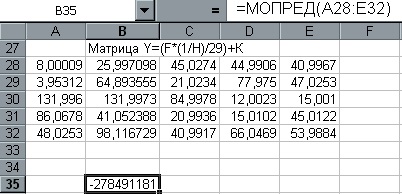
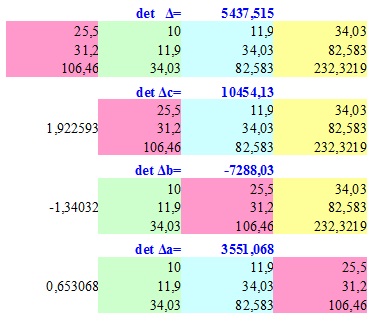
Procedura de calculare a determinantului sistemului cu matrice de ecuațiile de mai sus pentru un exemplu specific al unei parabole de ordinul a doua metoda celor mai mici pătrate, vezi
Calculul determinantul matricei transpusa a se vedea ajustarea p.V sezonieră a seriilor de timp
A se vedea, de asemenea, pe această temă: