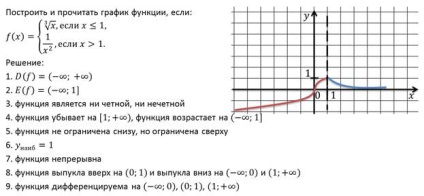
Rădăcina n-grad a unui număr nenegativ este un număr negativ, atunci când este ridicată la n-numărul de rotații pe care gradul de o.
Rădăcina de n-grad impar de numere negative este numit un număr negativ, atunci când a ridicat la n-numărul de rotații pe care gradul de o.
În cazul în care n - este un indicator al rădăcinii, și - un radicand.
Astfel, orice extract de rădăcină (pe a doua și mai mult) pot fi de orice numere non-negative și un număr negativ este extras din rădăcină doar grad impar.
La [0; + ∞) pot fi furnizate pentru fiecare număr x conform rădăcinii Singular de gradul n-x pentru orice valoare a lui n.
Adică, aceasta înseamnă că pe platoul de filmare [0; + ∞) putem vorbi de funcția rădăcină:
Acum definim proprietățile acestei funcții și se construiește graficul acesteia.
Proprietățile de bază ale funcțiilor:
Intervalul [0; + ∞) - un domeniu.
Deoarece număr non-negativ este rădăcina n grade de număr non-negativ, atunci intervalul [0; + ∞) este domeniul valorilor funcției.
Deoarece setul simetric nu este domeniul funcției, astfel încât funcția nu este nici ciudat, nici măcar.
Operația de extragere a rădăcinii a fost administrată ca o operație inversă ridicării la un nivel adecvat.
Deci, se poate argumenta că:
Acum puteți complot funcția rădăcină.
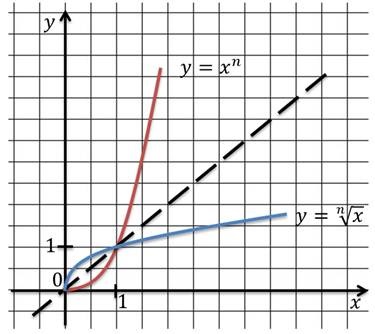
Folosind grafic, putem scrie proprietățile rămase ale funcției.
In intervalul [0; + ∞) crește funcției.
Funcția Top nu este limitată, dar este limitată de mai jos, de exemplu, o linie dreaptă de la care = -0.5.
Întregul domeniu al funcției este convexă în sus.
Am caracteristica cea mai mică valoare va fi 0, iar cea mai mare valoare are.
Dacă fiecare dintre punctele de unele funcții interval este diferențiabilă, aceasta înseamnă că o anumită perioadă este continuă.
În orice moment în intervalul [0; + ∞) există, acest derivat, singura excepție este punctul 0. Deoarece în orice punct din intervalul (0;) funcția + ∞ are un derivat, înseamnă pe intervalul (0;) funcția + ∞ este diferențiabilă.
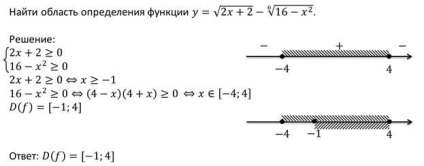
Luați în considerare câteva exemple de funcții de rădăcină grafice.
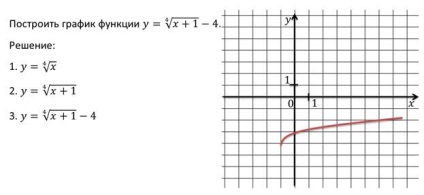
Aceste exemple se referă la funcția pentru care y este rădăcina gradul n-x, numai pentru valori non-negative ale argumentului.
Dar dacă n este un număr impar, atunci are x negativ și sensul expresiei rădăcină n grade de x. Deci, poți vorbi despre funcția:
Se înregistrează proprietățile acestei funcții.
Span (- ∞ + ∞) este domeniul funcției.
Span (- ∞ + ∞) este intervalul de valori.
Domeniul funcției este un set simetric, paritate, atunci această funcție poate fi studiată:
Astfel, vom vedea că funcția este impară pentru n impar.
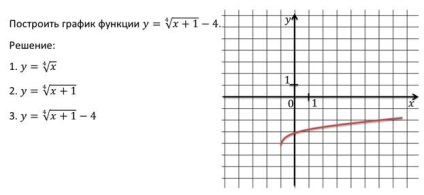
Noi construim graficul funcției.
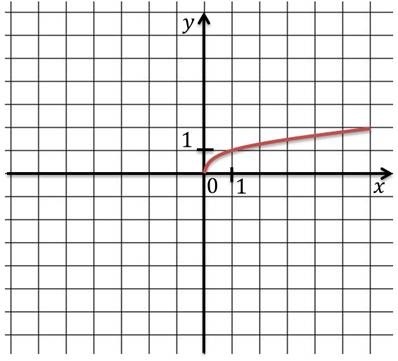
Noi adăugăm la această ramură are o ramură care este simetric față de origine, pentru aceasta folosim proprietatea funcției rădăcină ciudat.
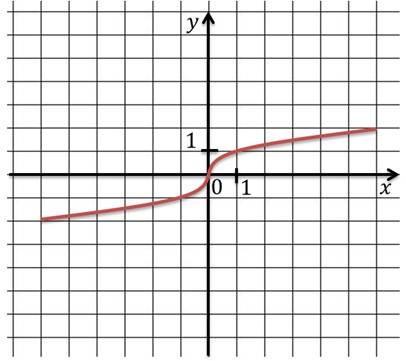
- Graficul rezultat a vă permite să înregistrați cu ușurință proprietățile rămase ale funcției.
- Întregul domeniu al funcției crește.
- Nici partea de sus, nici partea de jos a funcției nu este limitată.
- Funcția nu are cele mai mari și cele mai mici valori.
- Întregul domeniu al funcției este continuă.
- Intervalul (- ∞, 0) este convexă în jos, iar intervalul (0; + ∞) este convex în sus.
- Întregul domeniu al funcției este diferențiabilă, cu excepția punctului 0.
Câteva exemple de mai multe funcții grafice rădăcină.