
Această unitate este legată la 6 bari pătrați. Barele au caneluri, care fac posibile și trecere baruri din centrul nodului. Una dintre bare nu are caneluri, este pus în ultimul nod, iar la demontare se îndepărtează mai întâi.
Cumpara unul dintre aceste puzzle-uri pot fi, de exemplu, my-shop.ru
Varietatea de noduri sângeroase
Înainte de începutul secolului, câteva sute de ani de existență jucării în China, Mongolia, India, și a fost inventat mai mult de o sută de variante ale puzzle-ului, care diferă în configurația crestăturilor în baruri. Dar cele mai populare sunt două opțiuni. Se arată în figura 1 este rezolvată destul de ușor, pur și simplu și să-l. Este această structură folosită în vechiul sicriu indian. Dintre barele din Figura 2 este format de puzzle este numit „nod Diavolului“. După cum s-ar putea imagina, numele a primit pentru decizii dificile.
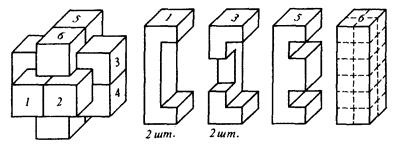
Fig. 1 Cea mai simplă versiune de „nod sângeroase“ Jigsaw
În Europa, în cazul în care, de la sfârșitul secolului trecut, „nodul Diavolului“, a câștigat popularitate, entuziaști au început să se gândească și de a face seturi de bare cu diferite configurații de decupaje. Unul dintre kit-ul cel mai de succes produce 159 puzzle-uri și este format din 20 bare de 18 specii. In timp ce toate nodurile sunt identice în aparență, ele sunt destul de diferit aranjate în interior.
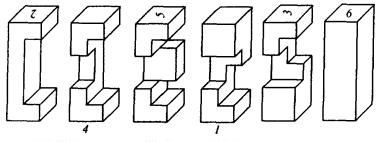
Fig. 2 "Golovlomka Admiral Makarov"
Stăruitor toate în această căutare a fost un profesor olandez de matematica Van De Boer, care, cu propriile sale mâini a făcut o colecție de câteva sute de bare și tabele compilate care arată modul de a asambla 2906 opțiuni noduri.
Acesta a fost în anii '60, iar în 1978 matematicianul american Bill Cutler a scris un program pentru calculator, și forța brută a stabilit că există 119,979 opțiuni de puzzle-uri de 6 elemente, combinații de proeminențe și adâncituri diferite în baruri, precum și plasarea bare, cu condiția că nu golurile din interiorul nodului.
Un număr surprinzător de mare pentru o astfel de jucărie mică! Prin urmare, pentru a rezolva problema și a avea nevoie de un calculator.
Pe măsură ce computerul rezolva puzzle-ului?
Desigur, nu ca o persoană, dar nu într-un mod magic. Computer rezolvă puzzle-uri (și alte obiecte) pe program, programatorii să scrie programe. Scrie, așa cum le convine, dar astfel încât să fie clar și calculatoare. Cum poate un calculator manipuleaza bare de lemn?
Noi pornim de la faptul că avem un set de bare 369, care diferă de la fiecare alte configurații ale protuberanțele (primul set de identificat Van De Boer). Computerul trebuie să introducă o descriere a acestor bare. Locașul minimă (sau protuberanța), în bar - un cub cu latura de grosime 0,5 bari. Să-l numim un singur cub. In general, astfel de bar 24 conține un cub (Figura 1). Calculatorul pentru fiecare bara Începe matrice „mici“ de 6h2h2 = 24 numere. O bară cu crestături secvență de 0 și 1 definit în matrice „mici“: 0 corespunde sculptat cub, 1 - întreg. Fiecare dintre matricele „mici“ are numărul propriu (1-369). Oricare dintre ele poate fi alocat unui alt număr de la 1 la 6, care corespunde poziției barei din interiorul puzzle-ului.
Ne întoarcem acum la puzzle. Imaginați-vă că se potrivește în interiorul unui cub 8h8h8 de măsurare. In acest cub calculator corespunde unei matrice „mare“, format din celule 8h8h8 = 512 numere. Pune niste bar in interiorul cubului - înseamnă să umple în celula matrice corespunzătoare „mare“ de un număr egal cu numărul de bar.
Comparând 6 matrice „mici“ și de bază, un calculator (E. Programul de ex.,), Deoarece adaugă împreună cele 6 baruri. Conform rezultatelor adăugarea de numere determină cât de mult și ce fel de „gol“, „umplut“ și „celule supraaglomerate“, formate în matrice principală. celula „Blank“ corespund spațiul gol din interiorul puzzle-ului, „umplut“ - care corespunde proeminențelor în baruri, și „aglomerat“ - o încercare de a combina două singur cub, care, desigur, interzise. O astfel de comparație este făcută în mod repetat, nu numai cu diferite baruri, dar, de asemenea, având în vedere rândul lor, locurile pe care le ocupă într-o „cruce“, și așa mai departe. N.
Ca rezultat, selectați acele opțiuni, care nu sunt celule goale și supraaglomerate. Pentru a rezolva această problemă ar fi suficient de „mare“ celule 6h6h6 dimensiune matrice. Se pare, totuși, că există combinații de bare, umplând complet volumul intern al puzzle-ului, dar ele nu pot fi demontate. Prin urmare, programul trebuie să fie în măsură să verifice nodul cu privire la posibilitatea de demontare. În acest scop, Cutler și a luat o serie 8h8h8, deși dimensiunea acesteia nu poate fi suficient pentru a testa toate cazurile.
El este umplut cu detalii despre puzzle-uri variante. În cadrul programului matrice încearcă să „muta“ barele, T. E. Se deplasează în matrice „mare“ de dimensiunea barei 2h2h6 celule. Cilindree are loc la o celulă în fiecare din cele 6 direcția paralelă cu axele puzzle-ului. Rezultatele celor șase încercări de care nu se formează celule „aglomerate“ sunt stocate ca poziția inițială pentru următoarele sesari încercări. Arborele rezultat este construit din toate mișcările posibile atâta timp cât orice bloc nu este în totalitate în afara corpului principal sau după toate încercările de a rămâne celule „aglomerate“, care a fost cea care nu poate fi demontată.
Asta au fost obținute prin calculator 119 979 versiuni ale „Nodul Diavolului“, inclusiv nu 108, așa cum anticii, iar versiunea 6402 cu 1 întreg, fără tăieturi bar.
Rețineți că Cutler a renunțat la problema generală - atunci când un nod conține atât goluri interne. În acest caz, numărul de noduri de 6 bare este mult crescută și căutarea exhaustivă necesară pentru a găsi soluții fezabile, este nerealist, chiar și pentru calculator moderne. Dar, așa cum vom vedea acum, cele mai interesante și provocatoare puzzle-a găsit în cazul general - dezasambla puzzle, atunci puteți face o departe de banală.
Datorită prezenței de goluri, este posibil să se deplaseze secvențial câteva bare înainte de a va fi capabil să separe complet orice bar. Mutarea bara decuplează unele bare, permite deplasarea barei următoare, și în același timp se angajează celelalte bare.
Cu cât trebuie să faceți manipulări în timpul demontării, cu atât mai interesantă și mai dificilă versiune a puzzle-ului. Canelurile din bare sunt aranjate, astfel încât cunningly căutarea de soluții amintește că rătăcind labirintul întunecat în care tot timpul veni împotriva ceva pe perete, apoi se termină mort. Acest tip de nod este, fără îndoială, merită un nume nou; vom numi „supernode“. măsură complexitatea supernodes se numește numărul de mișcări de bare individuale, care trebuie să se facă înainte de primul membru este separat de puzzle.
supernodes soluție
Produce desene astfel de puzzle-uri dificile ca supernodes, și să nu dezvăluie secretele lor ar fi prea crud chiar și cunoscătorilor de puzzle-uri. Vom emite o decizie supernodes într-o formă compactă, dreptunghiulară.
Înainte de a dezasambla ia puzzle-ului și se orienteze astfel încât să corespundă desen numere de piese 1. secvență dezasamblarea este înregistrată ca o combinație de cifre și litere. Numerele reprezintă numărul de bare, litere - direcția de deplasare, în conformitate cu cea prezentată în figurile 3 și 4, sistemul de coordonate. Scor de mai sus o mișcare în direcția negativă a axei de coordonate. Un pas - este mișcarea barei de 1/2 din lățimea sa. Când bara este deplasat două trepte dintr-o dată, mișcarea sa este scrisă în paranteze cu exponent 2. Când deplasate mai multe părți care sunt angajate unele cu altele, le incheie numerele n paranteze, de exemplu (1, 3, 6) x. bar Separarea puzzle-ului este marcat printr-o săgeată verticală.
Noi acum dau exemple de cele mai bune supernodes.
Puzzle W. Cutler ( "spin Bill")
Se compune din 1, 2, 3, 4, 5, 6, așa cum se arată în figura 3. De asemenea, dat algoritm soluție. Interesant, în revista «Scientific American» (1985, numărul 10) este o versiune diferită a puzzle-ului și este raportat că „spin Bill“ are o soluție unică. Diferența dintre variantele - doar un bar: 2 și 2 detaliu în figura 3.
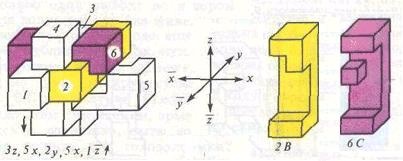
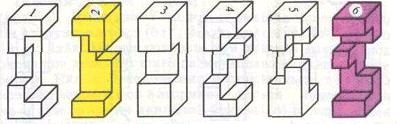
Fig. 3 „Barb Bill“, proiectat de un calculator.
Datorită faptului că partea 2 conține mai puține tăieturi decât piesa de prelucrat 2, introduceți-l în „spin Bill“, la cele de mai sus în Figura 3, algoritmul nu reușește. S-ar putea presupune că puzzle-a «Scientific American» merge într-un alt mod.
Filippa Dyubua puzzle (Fig. 4)
Se rezolvă în 7 se mută la următorul algoritm: (6 z) ^ 2, 3 x. 1 z. 4x, 2x, 2Y, 2z. Ha figură arată locația pieselor de pe dezasamblarea B mare. Pornind de la această poziție, folosind ordinea inversă a algoritmului și de a schimba direcția de mișcare în direcția opusă, se poate asambla puzzle.
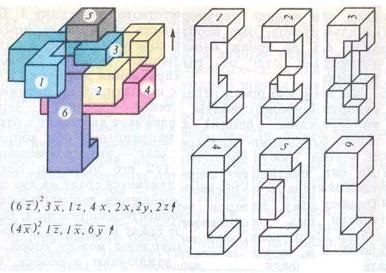
Fig. 4 supernode F. Dyubaya complexitate 7
Trei supernodes D. Vakarelova.
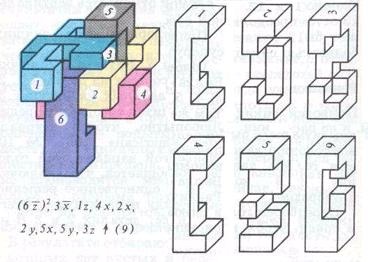
Fig. 5 supernode de 9 D.Vakarelova
Primul dintre puzzle-uri sale (Figura 5.) - este o versiune îmbunătățită a puzzle-ului Dubois, el are dificultăți 9. Acest lucru supernode mai mult decât altele, cum ar fi un labirint, ca atunci când demontarea apar miscari false impasuri interesante. Un exemplu de astfel de impas - x mișcări W. Z 1 la începutul dezasamblarea. O soluție corectă este:
(6 z) ^ 2, W x, 1z, 4x, 2x, 2y, 5x, 5y, 3z?.
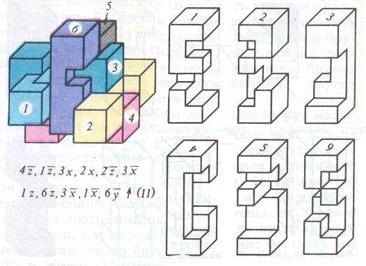
Fig. 6 supernode D. Vakarelova 11
(. Figura 6) Al doilea puzzle Vakarelova D. este rezolvată prin formula:
4 z, 1 z. Sx, 2, 2 z. lui W. 1Z, 6Z, Z x. 1 x, 3z?
și are complexitate 11. Este remarcabil faptul că bara 3 a treia mișcare ia un pas Sx și înapoi (B x) returnează a șasea viteză; și 1 bar, în a doua etapă se mută la 1 z. 7 și face cursul unui accident vascular cerebral întoarcere.
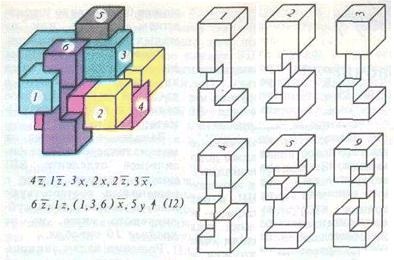
Fig. 7 supernode D. Vakarelova 12
Al treilea puzzle (Figura 7.) - una dintre cele mai dure. Solutia sa:
4 z. 1 z. Sx, 2, 2 z. lui W. 6 z. 1Z, (1,3,6) x. 5Y?
până în a șaptea cursa repetă puzzle-ului precedent, apoi, pentru a merge 9 acolo apare o situație complet nouă: dintr-o dată toate barele opresc în mișcare! Și atunci trebuie să se mute imediat pentru a ghici 3 bari (1, 3, 6), iar în cazul în care această mișcare este considerată ca fiind de 3 ture, atunci complexitatea puzzle-ului va fi egal cu 12.