Sistemul de ecuații algebrice liniare cu necunoscute - un sistem de ecuații ale formei
Aici - necunoscut care urmează să fie determinată. Sistemul Coeficienți „/> și se presupune că termenii săi liberi să fie cunoscută. Indicii Coefficient“ /> sistem desemnat numărul de ecuații și necunoscute, în care factorul de cost.
Sistemul se numește omogen. dacă toți termenii săi constante sunt zero, sau - non-uniformă.
Sistemul se numește un pătrat. în cazul în care numărul de ecuații este egal cu numărul de necunoscute.
Soluția sistemului - un set de numere astfel încât fiecare substituție în locul sistemului atrage toate ecuațiile sale în identități.
Sistemul se numește în comun. dacă are cel puțin o soluție, și inconsistente. dacă nu are nici o soluție. Sistemul comun poate avea una sau mai multe soluții.
Soluții și sistem de colaborare numit diferite. În cazul în care a încălcat cel puțin una din ecuațiile:
Sistemul comun se numește sigur. dacă are o soluție unică; în cazul în care are cel puțin două soluții diferite, este numit nedeterminată. Dacă ecuația este mai mare decât necunoscutul, este numit supradeterminat.
matriceal
Sistemul de ecuații liniare pot fi reprezentate în formă de matrice ca
Un exemplu al unui sistem de ecuații liniare
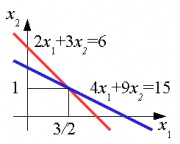
Soluție grafică a unui sistem de ecuații liniare
Sistemul de două ecuații cu două necunoscute este dată de
Pentru a găsi necunoscutul să fie rezolvată în ceea ce privește ecuația superioară: x_2 „/> și apoi substitui soluția rezultată în ecuația de jos: x_2 \ dreapta) + 9x_2 = 15.“ /> Soluția „/>.
Acest sistem poate fi reprezentat vizual pe grafic sub forma a două linii. Punctul cu coordonatele 1) „/> este o soluție.
metode de soluție
Metode directe (sau exacte) de soluții de sisteme liniare ajuta să găsească o soluție pentru un anumit număr de pași. Metodele directe includ metoda Gauss. Gauss - Jordan metoda Cramer, o metodă de matrice și matura (pentru matricea tridiagonal) metoda.
Metode iterative bazate pe utilizarea unui proces iterativ. Acestea vă permit să obțineți o soluție prin aproximări succesive. Prin metode iterative includ metoda de Jacobi (iterația simplă), Gauss - metoda de relaxare Seidel și Multigrid.