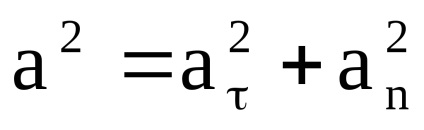Cea mai simplă formă de mișcare a unei mișcări mecanice. Reprezintă schimbarea poziției corpului sau a unor părți ale acesteia în spațiu, adică în raport cu celălalt. Sarcina principală a mecanicii este răspunsul la întrebarea: în cazul în care va fi amplasat în organism ne interesează timp.
Orice mișcare în mecanica poate fi reprezentat ca o combinație de două tipuri de bază de mișcare: translație și rotație.
Luați în considerare cel mai simplu caz de mișcare de rotație: rotirea unui corp rigid în jurul unei axe fixe.
Corpul este declarat a fi absolut solide, în cazul în care distanța dintre oricare două puncte de constant sale. Este clar că acest concept este o abstracție fizică. Într-adevăr satisface această condiție a corpului, deformarea poate fi neglijată în rezolvarea unor probleme.
Prin rotirea diferitele puncte ale corpurilor solide deplasează pe cercuri ale căror centre formează o linie. Această linie se numește axa de rotație. Este ușor de observat că deplasările unghiulare ale tuturor punctelor pentru aceeași perioadă de timp t sunt astfel la fel. Din acest motiv, poziția de rotație a corpului, este recomandabil să se determine unghiul la care este rotit în raport cu poziția sa inițială. Ecuația mișcării de rotație, în acest caz, va funcționa = f (t), care va avea aceeași formă pentru toate punctele corpului. Obținem o expresie a acestei funcții într-o formă generală. În acest scop, este suficient să se ia în considerare mișcarea unuia dintre punctele corpului în jurul axei.

În măsurarea SI unghiului produs în radiani. Unghiul în radiani 1 - este unghiul central care se sprijină pe lungimea arcului egală cu raza r a cercului. Ie pentru a determina unghiul in radiani lungime arc necesar împărțit la raza de curbură:
Luați în considerare parametrii cinematici de bază ale mișcării de rotație. Lăsați un interval de timp infinit mic punct material dt din poziția M este mutat în poziția

Colțul skorost- acest vector este numeric egal cu unghiul de rotație al vectorului rază


Timpul pentru care organismul face o rotație completă se numește perioada de rotație (T). pentru că unghiul de rotație corespunde unei rotații complete = 2 rad, apoi în mișcare uniformă
Valoarea egală cu numărul de rotații ale corpului pe unitatea de timp se numește frecvență de rotație n:
Ecuația mișcării de rotație uniformă (ω = const), obținută prin rezolvarea ecuației diferențiale (2):
Atunci când viteza de rotație neuniformă a schimbării vitezei unghiulare caracterizată prin accelerația unghiulară:


În cazul general, ecuația de mișcare de rotație uniform accelerată (β = const) pot fi obținute prin rezolvarea ecuației diferențiale
nenie (6) relativ :
puteți utiliza familiare parametrii cinematici liniare pentru a descrie mișcarea într-un traseu circular. De exemplu, viteza de deplasare a unui punct de pe traiectoria:
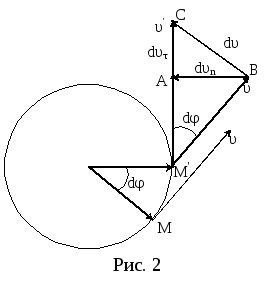
Această viteză la trecerea de la un punct de traiectorie (M) la altul (
extinde vectorul
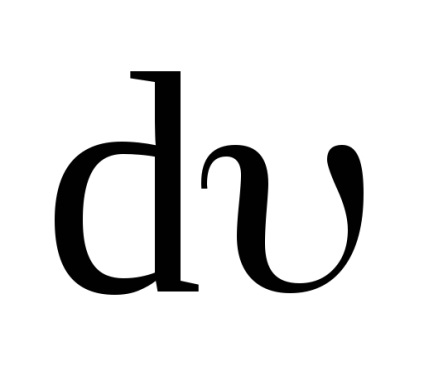
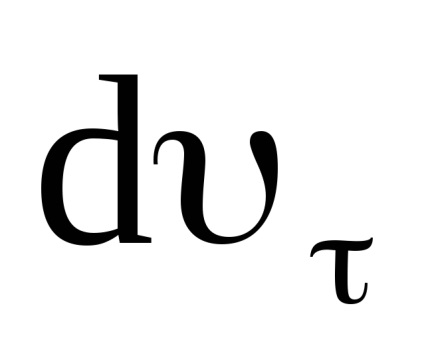
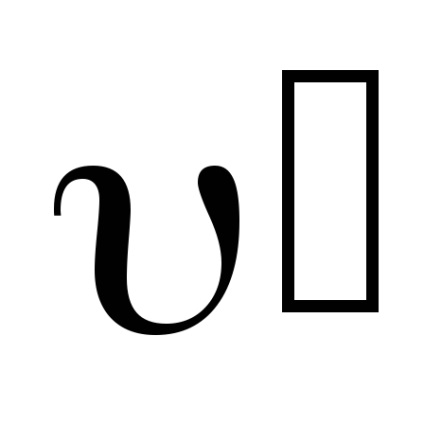
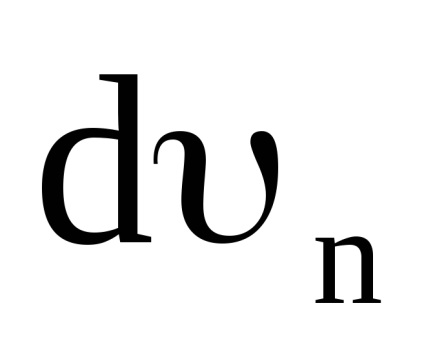
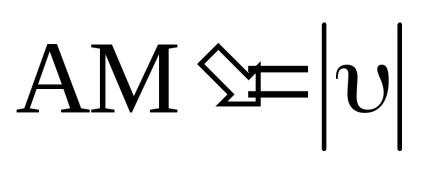
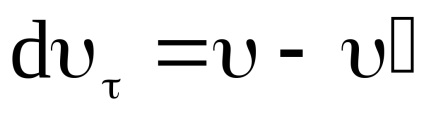
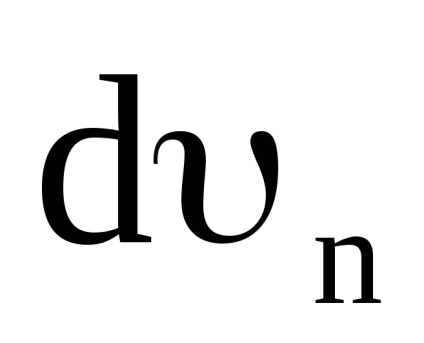
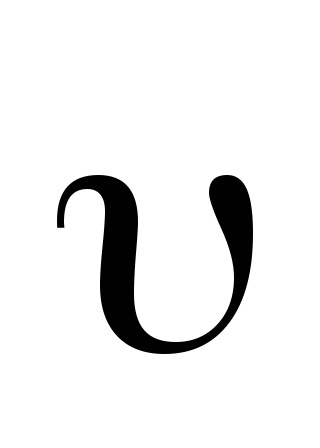
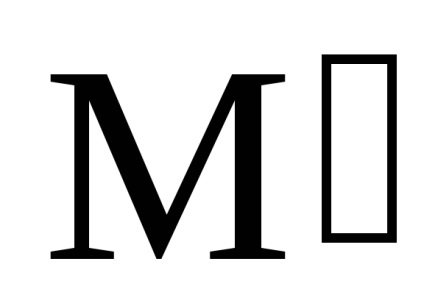
Împărțind (11) de către dt, obținem:
deoarece
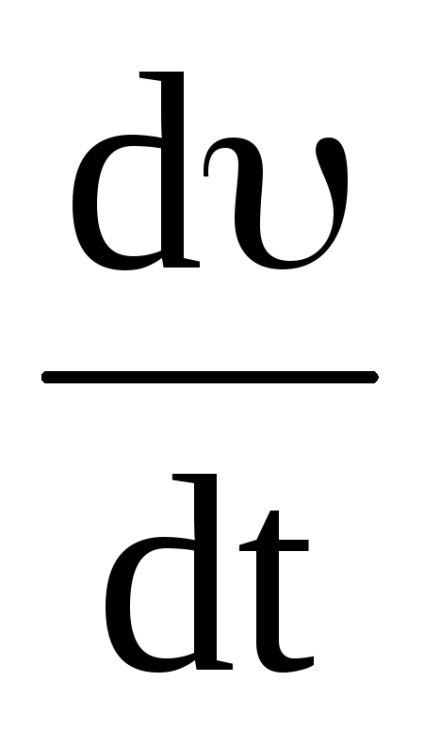

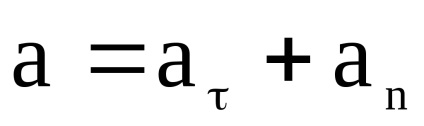
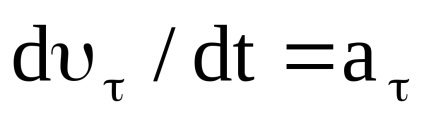
Stabilirea relației dintre parametrii de mișcare liniară și unghiulară circumferențial. Din relația (1)
Diferențierea dreapta și partea stângă a lui t, avem:
Această formulă definește modulul relație de colț liniar de viteză i modulul skorosti. Diferențierea (15), încă o dată de t, obținem pentru accelerația tangențială:
triunghiul
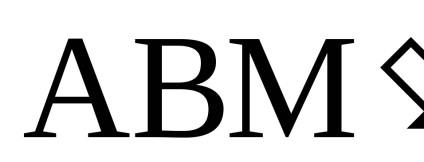
dn = · sind = · d. dar
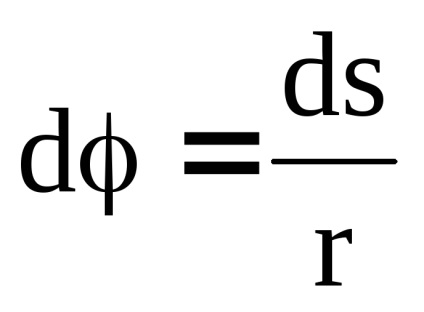
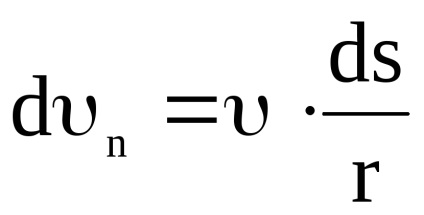
Diferențierea tpravuyu și partea stângă a acestei ecuații, obținem:
Având în vedere (15) din (17) obținem:
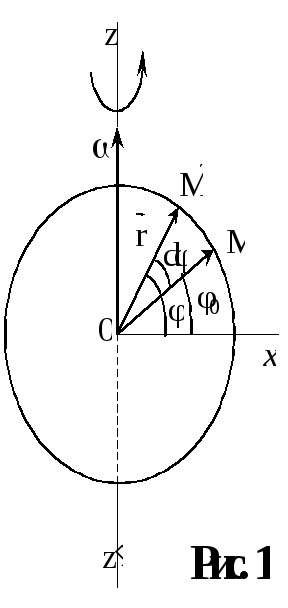
De la AVS (dυ) 2 = (dυτ) 2 + (dυn) 2 sau după divizare prin (dt) 2 -