Până în prezent, ne-am uitat la structura de date, datele care sunt aranjate liniar. Într-o listă legată - de la primul nod la un singur ultima. Dinamic matrice - sub forma unui bloc continuu.
În această parte ne vom uita la o nouă structură de date - lemn. Mai precis, binar (binar) arborele de căutare (binar de căutare copac). Binar copac de căutare are o structură arborescentă, dar elementele din ea sunt aranjate în funcție de anumite reguli.
În primul rând, considerăm un arbore normal.
Arbore - o structură în care fiecare nod poate avea zero sau mai multe sub-ansambluri - „copii“. De exemplu, un copac ar putea arăta astfel:
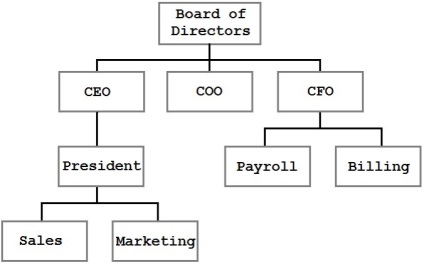
Acest arbore arată structura companiei. Nodurile reprezintă persoane fizice sau unități, linie - link-uri și relații. Arborele - acesta este cel mai eficient mod de prezentare și de stocare a acestor informații.
arbore binar de căutare
Binar copac de căutare este similar cu exemplul de mai sus copac, dar construite în conformitate cu anumite reguli:
- Fiecare nod nu este mai mult de doi copii.
- Orice valoare mai mică decât valoarea nodului devine copilul stâng al copilului la stânga sau la un copil.
- Orice valoare mai mare sau egală cu nodul devine copilul dreapta sau copilului dreptul copilului.
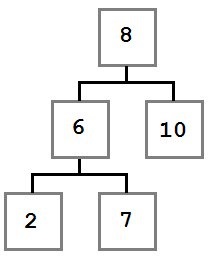
Să ne uităm la un copac, construit în conformitate cu aceste reguli:
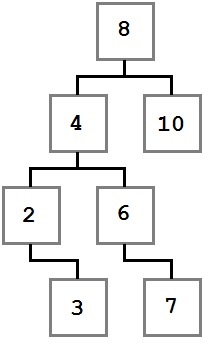
arbore binar de căutare
Notă modul în care aceste restricții afectează structura de lemn. Fiecare valoare este lăsată rădăcinii (8) este mai mic de opt, fiecare valoare pe dreapta - este mai mare sau egală cu rădăcina. Această regulă se aplică la orice nod al arborelui.
Cu aceasta în minte, să ne imaginăm cum se poate construi un copac. Deoarece primul copac a fost gol, prima valoare adăugată - opt - a fost de rădăcină.
Nu știm exact în ce ordine celelalte valori adăugate, dar poate reprezenta una dintre căile posibile. Nodurile se adaugă la metoda Add. care primește valoarea adăugată.
Să luăm în considerare primii pași.
În primul rând, a adăugat 8. Această valoare devine rădăcina copacului. Apoi am adăuga 4. Deoarece 4 este mai mică de 8, am pus-o în partea stângă a copilului, în conformitate cu regula 2. Deoarece nodul cu opt copii lăsat, 4 este singurul copil din stânga.
Apoi, vom adăuga 2 2 mai puțin de 8, așa că vom merge la stânga. Deoarece stânga au deja o valoare, l-am compara cu introdus. 2 este mai mic de 4, iar la patru nu au copii la stânga, astfel încât 2 devine copilul stânga 4.
Apoi vom adăuga primele trei. Ea merge la stânga de 8 și 4. Cu toate acestea, din moment ce 3 este mai mare de 2, devine Drepturile Copilului 2, în conformitate cu a treia regulă.
comparații secvențială Inserează cu un potențial părinte continuă până când, până când găsiți locul pentru a insera, și se repetă pentru fiecare plug-in-materie, atâta timp cât nu toate întregul copac va fi construit.
clasa BinaryTreeNode
Eliminați metoda
- Comportament: Îndepărtează primul nod la o valoare predeterminată.
- Complexitatea: O (log n), în medie; O (n), în cel mai rău caz.
Ștergerea unui nod din arborele - una dintre acele operațiuni care par simple, dar, de fapt, plină cu multe capcane.
În general, algoritmul pentru ștergerea elementului este după cum urmează:
- Găsiți nodul pe care doriți să-l ștergeți.
- Scoateți-l.
Primul pas este destul de simplu. Considerăm că căutare conține nod în metoda de mai jos. Odată ce am găsit un site pe care doriți să o eliminați, avem trei cazuri posibile.
Cazul 1: În nodul șters nu are nici un copil drept.
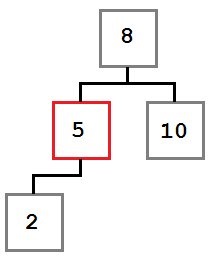
În acest caz, vom muta pur și simplu stânga-copil (dacă există) la locul nodului șters. Ca rezultat, copacul va arata astfel:
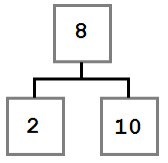
Cazul 2: În nodul șters are doar copilul drept, care, la rândul său, nici un copil din stânga.
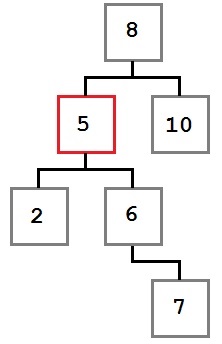
În acest caz, trebuie să ne mișcăm drepturile nodului copilului care urmează să fie eliminat (6) în locul său. După îndepărtarea copacului va arăta astfel:
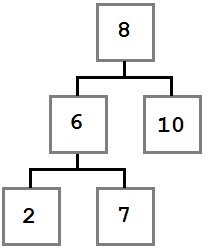
Cazul 3: În nodul șters este primul copil, care este un copil stânga.
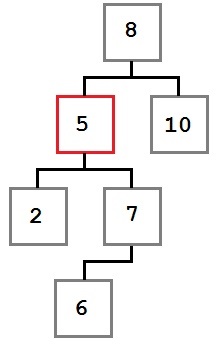
În acest caz, plasați nodul îndepărtat ocupă extremitatea stângă copil al nodului copil dreptul de a fi eliminate.
Să vedem de ce este așa. Știm despre subarbore pornind de la nodul care urmează să fie eliminate după cum urmează:
- Toate valorile la dreapta mai mare sau egală cu valoarea nodului.
- Cea mai mică valoare a subarborelui drept - la stânga.
Am pus în aplicare dozhny eliminat nod cu o valoare mai mică sau egală cu orice nod de pe dreapta. Pentru a face acest lucru, trebuie să găsim cea mai mică valoare din subarborele din dreapta. De aceea, vom lua nodul mai din stânga a subarborelui drept.
După îndepărtarea copacului nodul va arata astfel:
Acum, că știm cum să ștergeți noduri, uita-te la codul care implementează algoritmul.
Rețineți că metoda FindWithParent (a se vedea. Metoda Contains) returnează un nod găsit și mamă, pentru că trebuie să înlocuim nodul părinte al copilului stânga sau la dreapta lui îndepărtată.
// Dacă valoarea de bază este mai mare decât curentul,
// copil din dreapta al nodului curent devine copilul stâng al părintelui.
părinte. Stânga = curent. dreapta;
else if (rezultat <0 ) >> // Cazul 3: În cazul în care drepturile copilului au copii stânga, stânga copil al subarborelui drept // înlocuiește nodul șters. altfel // din stânga subarborelui drept subramificație al părintelui devine nodul stânga. leftmostParent.Left = leftmost.Right; // copil stânga și la dreapta al nodului curent devine din stânga și din dreapta copilului stânga. leftmost.Left = current.Left; leftmost.Right = current.Right; dacă (părinte == null) <_head = leftmost;> altfel
// Dacă valoarea de bază este mai mare decât curentul,
// nod devine cea mai din stânga copilul stâng al părintelui.
părinte. Stânga = stânga;
Traversarea copaci
Traversal de copac - o familie de algoritmi care permit să proceseze fiecare nod într-o anumită ordine. Pentru toți algoritmii de by-pass de mai jos, de exemplu, pentru a fi utilizat următorul pom:
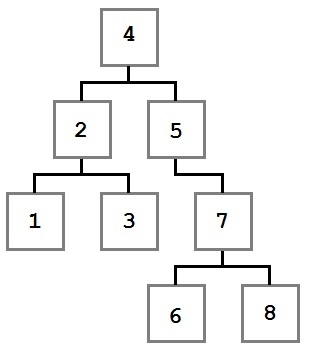
Exemplu arbore bypass
rezolvări în exemple vor accepta parametrul de acțiune
De asemenea, cu excepția pentru descrierea comportamentului și a complexității algoritmice a metodei se va face referire la ordinea valorilor obținute atunci când crawling.
Metoda Precomanda (sau by-pass prefix)
- Comportament: traversa copac pentru prefix, finalizați următorii pași pe fiecare nod.
- Complexitatea: O (n)
- Bypass Procedura 4, 2, 1, 3, 5, 7, 6, 8
Când algoritmul de prefix parcurgeri devine valoarea curentă a nodului înainte de prima trecere in subarborele din stânga, apoi spre dreapta. Pornind de la rădăcină, la început vom obține o valoare de 4. Apoi, în același fel costa copilul stânga și copiii lui, atunci copilul drept și toți copiii săi.
Prefixul este de obicei folosit pentru a ocoli lemnul copie cu păstrarea structurii sale.