Noi introducem conceptul de viteza unghiulară și accelerația unghiulară a unui corp. Dacă - un vector unitate îndreptat în direcția pozitivă a axei sale de rotație, vectorii de viteză unghiulară și accelerația unghiulară este determinată de expresiile:
Deoarece - constantă în vectorul magnitudine și direcția de la (63), care
Când și direcția vectorilor și sunt identici. Acestea sunt ambele îndreptate într-o direcție pozitivă de rotație axei Oz (Fig. 31 a). În cazul în care. ele sunt orientate în direcții opuse (fig. 32b). Vectorul accelerației unghiulare coincide cu direcția vectorului vitezei unghiulare cu rotație accelerată și opusă se la un proces lent. Vectori și pot fi reprezentate, în orice punct al axei de rotație.
Formula Vector pentru vitezele și accelerațiile punctelor corpului
Ne exprimăm viteza, forfecare, accelerația normală și punctele complete ale corpului într-o formă vectorială (Fig. 32). punct de magnitudine viteza și direcția poate fi reprezentată de produsul vectorial
în care - vectorul raza unui punct. trase dintr-un punct arbitrar al axei de rotație. de exemplu, punct. Expresia (75) se numește formula vectorul Euler.
Deoarece accelerația și vectorul Euler au formula:
Primul termen din (76) este accelerația tangențială, iar al doilea - normală, adică ..
mișcare complexă a unui punct
Pentru a explora unele tipuri mai dificile de mișcări ale corpului rigide adecvate pentru a lua în considerare doar o mișcare complicată a unui punct. În multe probleme de deplasare a punctului trebuie să fie luate în considerare în ceea ce privește două (sau mai multe) sisteme de referință, se deplasează în raport cu celălalt. Deci, mișcarea nave spațiale, se deplasează spre Lună, este necesar să ia în considerare atât în raport cu Pământul și Luna în raport cu care se deplasează în raport cu Pământul. Orice mișcare a punctului poate fi considerat ca un complex format din mai multe mișcări.
În cel mai simplu caz, o mișcare complicată a unui punct este format din mișcări portabile și relative. Definim aceste mișcări. Să presupunem că avem două cadre de referință care se deplasează în raport cu altele. Dacă una dintre aceste sisteme (fig. 33) este luată ca bază sau fixă (mișcarea acesteia în raport cu celelalte cadre nu este considerat), al doilea sistem de referință se va deplasa în raport cu primul. Punct deplasare în raport cu cadrul mobil numit relativă. Caracteristicile acestei mișcări, cum ar fi o traiectorie, viteza și accelerația sunt cunoscute ca relativă. Ele reprezintă un index; pentru viteză și accelerație și. punct în ceea ce privește mișcarea principală. sau fixe. Sistemul de referință se numește absolut (sau complex). Este, de asemenea, denumite uneori ca o mișcare de compus. Traiectoria, viteza și accelerația mișcării numite absolute. Viteza și mișcarea de accelerație absolută desemnate prin literele fără indici. mișcare portabil se referă la mișcarea cadrului de referință se deplasează în raport cu fix. Din cauza mișcării relative a punctului în mișcare la diferite intervale de timp coincide cu diferitele puncte ale corpului. la care este fixat un cadru mobil de referință. Viteza portabil și accelerare sunt viteza portabile și accelerația punctului a corpului. care, la momentul în care coincide punctul în mișcare. Viteza transportabil și accelerația, și reprezintă.
plus viteza de teoremă: viteza absolută a punctelor de mișcare este egală cu viteza suma vectorială a mișcărilor portabile și relative ale acestui punct
Deoarece, în general, și viteza portabile mișcări relative nu sunt perpendiculare, atunci
Viteza absolută poate fi scrisă ca:
este rata în termenii unui corp rigid liber, fixat la deplasarea sistemului de coordonate, care este în prezent același punct în mișcare a corpului în raport cu sistemul fix de axe. Acesta este punctul portabil de viteză.
Punct plus Teorema accelerare (cinematică Coriolis teorema). accelerația absolută a punctului este suma vectorială a celor trei accelerațiilor - portabile și relativ Coriolis
Accelerare se numește accelerația Coriolis. Uneori este, de asemenea, numit (sau de cotitură) accelerare suplimentară.
accelerația absolută poate fi, de asemenea scrisă ca:
În această formulă, primele trei termeni cuprind punctul de accelerație liberă solidă în cazul general al mișcării, împreună cu sistemul mobil de axe de coordonate față de staționare. Primul termen - accelerația punctului. și - respectiv, iar punctul normal de accelerare de rotație. în cazul în care doar mutat împreună cu bunul mobil sistem de axe, fără punctul considerat de coordonate în timp mișcării relative.
Cu titlu de definire a coordonatelor în coordonate carteziene
în care - coordonatele punctului în mișcare în raport cu sistemul de axe de coordonate în mișcare; - versorii axelor. Cu procesul sarcină de mișcare naturală
în care: - distanța de la origine la un punct de pe traiectoria mișcării relative; - raza de curbură a traiectoriei. În cazul particular când o mișcare portabil este de rotație în jurul unei axe fixe, accelerare portabile
unde accelerația tangențială a portabilului
în care: - cea mai mică distanță de la punctul de la axa de rotație în mișcare. accelerație medie portabil
Accelerația absolută în acest caz,
Se consideră accelerația Coriolis și proprietățile sale. Acesta este definit prin formula (81)
Viteza unghiulară a mișcării de rotație a sistemului de referință piesă mobilă, adică, viteza unghiulară a mișcării de translație, desemnată.
accelerația Coriolis este rezultatul influenței depunerilor reciproce a două mișcări: un portabil și relativă. O parte din aceasta se obține ca urmare a schimbărilor în viteza de deplasare a punctului de la mișcarea relativă. O altă parte din ea, de asemenea. este rezultatul modificărilor vitezei relative datorită mișcării de translație.
Modul Coriolis accelerație în conformitate cu (81), definit prin expresia
Pentru a determina accelerația Coriolis este regula foarte convenabil Zhukovsky N. E. Ea se bazează pe formula (81). Să avem un punct. se deplasează cu o viteză relativă. (Fig. 34). Am construi un avion. perpendicular pe viteza unghiulară de rotație a portabil. și de proiect pe acest plan. proiecția. Este un vector; modulul său
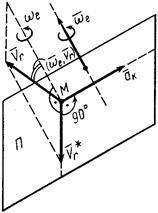
accelerația Coriolis este exprimat sub forma
Utilizarea (81) și (84 „), noi de obicei Zhukovskogo: modulul Coriolis accelerație este egală cu de două ori produsul vitezei unghiulare de rotație a modulului portabil proiecția vitezei relative pe un plan perpendicular pe axa de rotație a portabilului; pentru a obține o direcție a accelerării Coriolis, trebuie proiecția relativă vectorul vitezei rotit cu 90 ° în jurul unei axe paralele cu axa de rotație a unui portabil, în direcția de rotație.
Luați în considerare cazurile de atac la zero accelerația Coriolis. Din (84) rezultă că. în cazul în care:
1). și anume mișcare portabil este de translație;
2). și anume In acele vremuri, în care o schimbare în direcția mișcării relative;
3). și anume când viteza de deplasare relativă paralelă cu viteza unghiulară de rotație a portabil.