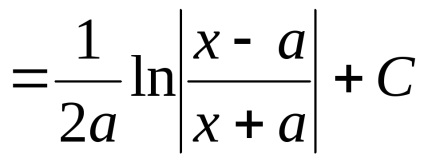I. Introducere factor constant în afara semnului integrală.
Factorul Teorema 3.Postoyanny poate fi luată ca un semn al unei integrale nedeterminată, și anume,
Dovada. Să luăm derivatul din partea dreaptă a (4.1) și să ia un factor constant pentru semnul derivatului:
.
Formula folosind (2.2). Din moment ce am descoperit că
,
care este, în partea dreaptă a (4.1) este un set de valori de bază pentru o funcție
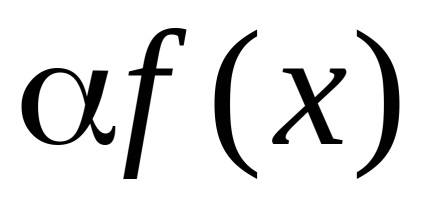
Exemple de aplicare a teoremei 3.
.
II.Predstavlenie integrală ca sumă a mai multor termeni.
Teorema 4.Neopredelenny integrantă suma algebrică a două funcții este egală cu suma algebrică a integralelor acestor funcții, și anume
Dovada. La fel ca și în dovada Teorema 3, vom diferenția partea dreaptă a ecuației (4.2). Având în vedere că derivatul unei sume algebrice egală cu suma algebrică a derivatelor, obținem
.
Așa cum am obține că
.
Astfel Teorema 4 este demonstrată.
Notă. Formula (4.2) poate fi extinsă la orice număr de funcții. La calcularea integralele în partea dreaptă (4.2), există mai multe constante arbitrare. Chiar sensul nedefinită integralei ca un set de valori de bază rezultă că nu este necesar să se scrie toate constante, și trebuie doar să introduceți o constantă arbitrară în expresia finală.
Aici exemple de aplicații comune Teoremelor 3 și 4.
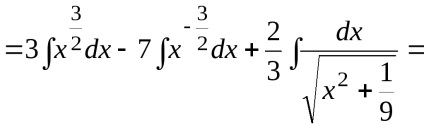
.
.
Următoarele exemple arată că integrandul este adesea necesară în primul rând convertit, să-l pregătească pentru aplicarea Teoremelor 3 și 4.
.
.
.
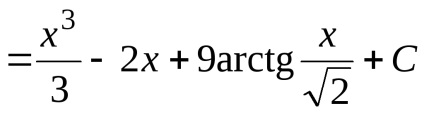
Teorema 5.Pust cunoscut faptul că
numerele gdeaib-
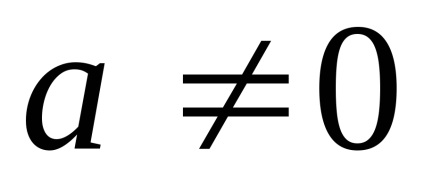
Dovada. Ca de obicei, distingem partea dreapta cu formula (4.3), și arată că este derivata funcției integrandul pe partea stângă. Rețineți că funcția
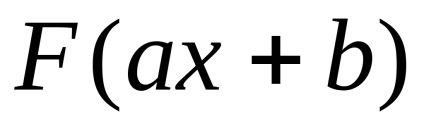
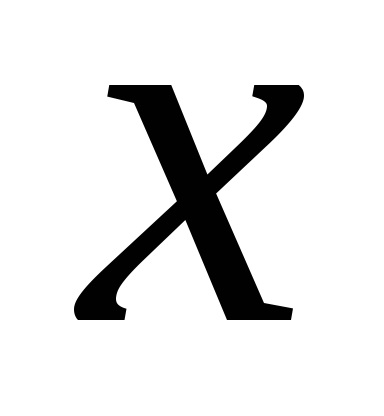
Apoi avem lanțul de egalități


Teorema 5 este demonstrată.
Rețineți că formula (4.3) pot fi obținute prin introducerea semnului integrală a unei variabile noi
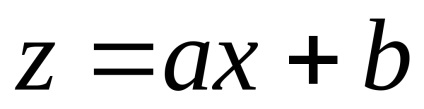
.
exprimând
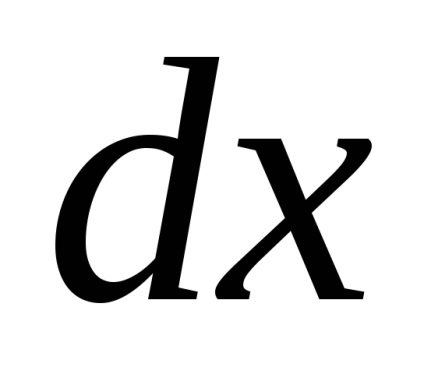
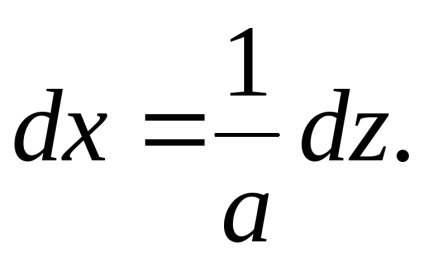
Deci, setați lanțul de egalități:
Este un lanț (4.4) și este convenabil să se utilizeze la calcularea integralele specifice. În același timp, introducerea unei noi variabile poate fi omisă, treceți la ultima egalitate.
Exemplul 4.10. Vom introduce o nouă variabilă. atunci
Exemplul 4.11 .. Vom introduce o nouă variabilă. Apoi.
,
În exemplele (4.14) și (4.15) integrands reprezentat anterior într-o formă care poate fi aplicată pentru a le Integrale masă.
.
Vom introduce o nouă variabilă. atunci
Vom introduce o nouă variabilă
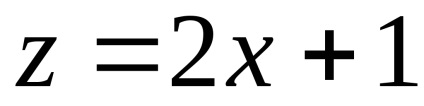
.
Referindu-ne acum la tabelul 1 și care provin penultimul trei integral, m. F. (3.13) și (3.14) și (3.15) prin intermediul teoremei 5.
Calculați integral (3.13) pe baza integralei (3.11) a tabelului.
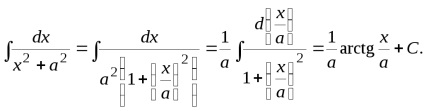
Integrala (3.14) se calculează pe baza integralei (3.12) a tabelului.
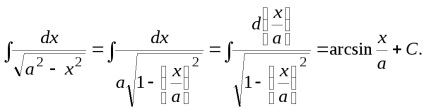
Pentru a calcula integralei (3.15), folosind integral tabular (3.3).