O scurtă descriere a documentului:
Acesta conține informații utile, complete și de înaltă calitate, care asimilare nu este împiedicată de nimic. Elevii maestru cu ușurință materialul de pe acest subiect, așa cum a luat în conformitate cu o serie de cerințe, inclusiv vârsta elevilor.
Pentru a învăța mai ușor să înțeleagă principiul de lectură grafice de funcții, este necesar să se reamintească faptul că argumentul este numit, adică variabila dependentă și variabila independentă. Apoi, este invitat să revizuiască unele funcții arbitrare și construi graficul acesteia prin găsirea unor perechi de numere care sunt coordonatele punctelor într-un sistem de coordonate. Atunci când programul este construit, a introdus definiția graficului funcției.
Lecția va fi utilă atât pentru profesori cât și pentru elevi.
Citirea graficul unei funcții numerice.
Citirea graficelor de funcții este de o mare importanță practică. În special, utilizarea de relații funcționale și diagrame este utilizat pe scară largă în economie.
Pentru studiul de subiect de astăzi, trebuie să ne amintim: ce funcție se numește numeric?
O funcție numerică este o regulă prin care fiecare element al setului de X de mare asociem un element unic al multimii y mari.
Setul X este domeniul funcției.
Set Y se numește setul de valori ale funcției.
Egalitatea y este de la X eff numită ecuația funcției.
x - variabilă independentă sau argument funcție. y - variabilă dependentă.
Ceea ce se numește graficul unei funcții?
Având în vedere o funcție y este egal cu ef x, unde X aparține X-mare, și să ia toate perechile de X, Y, și le-a pus sub punctul de coordonate relevante plan, obținem graficul. Grafic funcției - un grafic care arată relația dintre seturile de X este mare și y este mare.

Citiți programul - acest lucru înseamnă a transfera proprietățile funcției,
1) Domeniul funcției;
2) regiunea de valori;
3) zerouri funcție - valorile de argument pentru care funcția este zero;
4) intervale constante t.e.promezhutki funcției semn,
în cazul în care valorile funcției au același semn;
5) Intervalele funcției monotonie, adică, intervale unde creșterile funcției sau scăderile;
6) naibolsheei cea mai mică valoare a funcției, adică, cea mai mare și cea mai mică valoare a variabilei dependente;
Proprietățile care nu au toate caracteristicile:
9) chiar, impar;
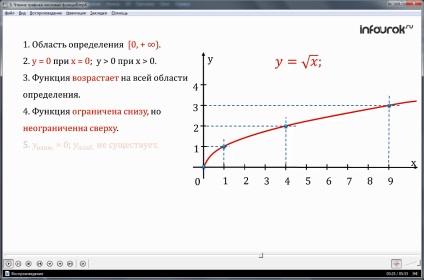
Citește graficele funcțiilor cunoscute, de exemplu, y este egală cu rădăcina pătrată a lui X.
1. Domeniul tehnic al definiției funcției -
fascicul de la zero la infinit plus
2. Y este egal cu zero pentru X egal cu zero; y este mai mare decât zero, atunci când X este mai mare decât zero.
3. Funcția este în creștere pe domeniul său.
4. Funcția este mărginită de mai jos, dar nu a fost legat de mai sus.
5igrek puțin egală cu zero se obține cu X egal cu zero; y cea mai mare există.
6.Funktsiya continuă într-un domeniu dat.
7. Domeniul de aplicare a valorilor - fascicul de la zero la infinit plus
8.Grafik convexitate orientată în sus.
y = kx + în

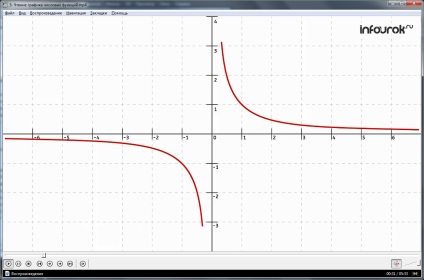
Citește graficul mărginit de funcții al cărui grafic, sunt reprezentate
1. Domeniul de definire a funcției - intervalul de la minus trei la trei.
2.Funktsiya are un zero: X este zero.
Funcția Valoarea 3.Polozhitelnye ia atunci când X este mai mare decât zero și mai mic sau egal cu trei. negativ - în cazul în care X este mai mare sau egal cu minus trei și mai mică decât zero ..
4.Oni în creștere, deoarece primul X X vtoroevypolnyaetsya Aeff mai puțin inegalitatea X este mai mică decât prima Aeff al doilea X.
5.Mnozhestvo un interval de valori de la minus unu la unu.
6.Sledovatelno, cea mai mică valoare a funcției este un minus, iar cel mai mare - unul.
7.Funktsiya mărginită de sus și mai jos.
interval de 8.The minus trei la zero funcție este în jos convexe, și
în intervalul de la zero la trei convexe în sus.
9.Nepreryvna pe întregul domeniu.