
Soluție: Este recomandabil să se ia în considerare cifra din unghiuri diferite: la fiecare două linii intersectate definesc un plan (lucrarea planul axiomă) → triunghi → paralelism și egalitate
laturile opuse ale proprietăților paralelogramului triunghi midline → A1B1C1D1 - paralelogram (prin definiție).
Eficacitatea procesului educațional depinde în mare măsură de capacitatea studenților de a dobândi în mod independent și să aplice cunoștințele. Problema unei tehnici de formare a abilităților de muncă independentă a studenților este relevantă pentru fiecare profesor de matematică. Predarea geometrie permite cea mai mare de a dezvolta capacitatea elevilor de muncă independentă, în special în rezolvarea problemelor. Elevii au nevoie pentru a genera diferite moduri de a crea imagini și de a le manipula.
Sarcini pentru a crea imagini geometrice utilizate în trei moduri:
crearea unei imagini vizuale;
schimba desen, având în vedere ca un produs finit în cursul rezolvării problemei;
modificarea desen mentală (pentru imagini) fără a schimba aspectul original.
Pentru a dezvolta capacitatea elevilor de a rezolva independent probleme geometrice, este necesar să se aibă materiale didactice (sarcini, exerciții), care ia în considerare specificul proiectarea imaginilor spațiale și de a le manipula.
Cunoașterea caracteristicilor specifice ale elevului profesor crea imagini geometrice îi permite să efectueze lucrări de remediere pentru a dezvolta gândirea spațială a elevilor în direcția cea bună.
dezvoltat în continuare o serie de probleme didactice de soi „crearea de imagine“, prin tragere pe tema. „Paralelismul în spațiu“ Sarcinile sunt defalcate în funcție de tipurile de lecții: învățarea noului material; aplicarea de cunoștințe și abilități; Testul de cunoștințe și abilități. Acesta conține o serie de sarcini sarcina de a traduce aceste sarcini verbale într-o imagine grafică; selectarea caracteristici esențiale concepte geometrice; izolarea figurilor compoziției desenului; în comparație cu cifrele (transformarea similaritate); luarea în considerare a cifrelor de desen din diferite puncte de vedere; modificarea poziției spațiale a structurii imaginii originale.
Toate sarcinile sunt date în formulare verbală, în scopul de a identifica capacitatea studenților de a crea o imagine spațială a descrierii verbale, egalizare astfel crearea imaginii de referință. Pentru fiecare sarcină sunt definiție aplicate, caracteristici, proprietăți concepte geometrice.
Studiul a subiectului „paralelismul în spațiu“ poate fi împărțit în 3 părți:
linie paralelă și un plan;
5.1. Lecții de învățare material nou
1.01. Asigurați-desen: Drept plan paralel MP # 945, și linia MT traversează acest plan într-un punct T (fig. 11).

1.02. Asigurați-un desen: plan # 945; intersectează trei linii drepte paralele a, b și c, respectiv, la punctele A, B și C care aparțin aceleiași linii (fig. 12).
1,03. Asigurați-un desen: plan # 945; Traversează trei linii drepte paralele a, b și c, respectiv, la nodurile # 8710; ABC (Figura 13.).
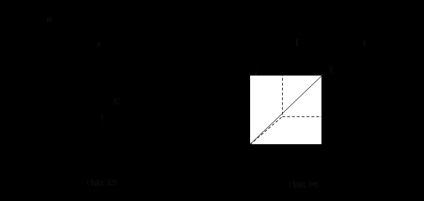
1.04. Egal cubic ABCDA1B1C1D1 (Fig. 14). 1) Selectați o margine în ea BB1 și numesc toate muchiile cubului: a) paralelă cu ea; b) trecerea acesteia; c) a trecut cu el. 2) Selectați diagonală fețele cub AD1 ADA1D1 și nume diagonală fețe: a) AD1 paralelă; b) trecerea acesteia; c) oblic cu ea. Justificați răspunsul.
2.01. Asigurați-un desen: plan # 945; Se trece prin punctele mediane ale laturilor AB și AC ale triunghiului ABC și nu conține vertexul A (fig. 15).
2.02. Asigurați-desen: Drept plan paralel MP # 945, și planul PMT intersectează planul în linie dreaptă CT (fig.16.).

2.03. Asigurați-vă de desen: direct și paralel cu fiecare dintre planurile paralele # 945; și # 946; (Fig. 17).
2,04. Este cunoscut faptul că linia m paralel cu planul # 945;. Este această linie paralelă cu orice linie dreaptă situată în planul # 945; (Fig. 18)? Justificați răspunsul.
Soluție: Lăsați linia și aparține avionul # 945;. Am ales să direcționeze m punct arbitrar M și trage prin ea și drepte și plane # 946; (Plan de referință Axiom). M drepte și nu cruce (prin ipoteză), atunci ele sunt fie paralele () sau incrucisate (). În consecință, drept, paralel cu linia m, vor fi doar cei cu care avionul poate fi setat (implicând m).

2.06. Luați în considerare două linii oblice a și b (fig. 19). Prin fiecare punct al liniei și o linie dreaptă paralelă cu linia b. Demonstrați că toate aceste linii se află în același plan. Cum este acest plan în raport cu linia B? Justificați răspunsul.
Soluție: Fie m || b. , Apoi m și definesc un plan și # 945;. Ia într-un plan # 945; directă cu || b. Pe baza liniilor paralele: a || m, atunci ele definesc un plan # 946;. Prin ipoteză, așa că, de asemenea, să definească un plan, care coincide cu # 945;. În consecință, toate liniile drepte paralele cu b și trecere și se află într-un plan, care, la rândul său, este paralelă cu b (pe baza unor linii paralele și avioane).
2.07. La punctul tetraedru ABCD K, F, N și M - nervurilor mijlocul respectiv AD, BD, BC și AC (Figura 20.). Completați tabelul de (cerc) ați specificat locația liniei specificate și planul: A - cruce, B - în paralel, în - linie se află în planul D - nu poate fi determinată:
Liniile și avioane