[2; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, ...]
(Această rolă continuă nu este periodică. Înregistrate în notație liniară)
Primele 1000 decimale ale e [1]

Aria de sub graficul y = 1 / x în intervalul 1 ≤ x ≤ e este 1
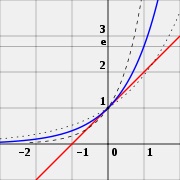
e - este un număr de. astfel încât valoarea derivatului (panta liniei tangente) a exponențială f (x) = a x (albastru), la punctul x = 0 este egal cu 1 (linia roșie). Prezentată pentru funcția comparație 2 x (curba punctată) și 4 x (linia punctată); panta tangentei care este diferit de 1
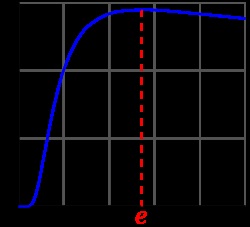
maximă este atinsă la funcția.
Deoarece exponentul funcția integrează și diferențiază „în sine“, logaritmi la baza e este luată ca fiind naturale.
Metode de determinare [citare]
Numărul de e poate fi determinat în mai multe moduri.
- După limita (a doua limita remarcabila). (Formula lui Stirling).
- Ca suma seriei. sau.
- Ca un singular. pentru care
- Ca doar numărul pozitiv. al cărui drept
Proprietăți [modifică]
Această proprietate joacă un rol important în rezolvarea ecuațiilor diferențiale. De exemplu, singura soluție a ecuației diferențiale este funcția, unde c - constanta arbitrare.- Numărul e este irațională și chiar transcendental. transcendența lui a fost dovedită numai în anul 1873 de către Charles Hermite. Se presupune că e - numărul normal. că este, probabilitatea de numere diferite în notele sale este aceeași.
Să presupunem că rațional. Apoi, în cazul în care - întregi, și - naturale.
Înmulțind ambele părți ale ecuației pentru a obține
Reporta pentru partea stângă:
Toți termenii de pe partea dreaptă a întregului, prin urmare, suma pe partea stângă - ansamblu. Dar această sumă este pozitivă, înseamnă că nu este mai mică de 1.
Pe de altă parte,
Rezumând progresia geometrică în partea dreaptă, obținem:
- Numărul e este calculabil (și, prin urmare aritmetică) numărul.
- , cm. Formula lui Euler. în special
- Mai multe formule privind numărul și e tt:
- t. n. „Poisson integrală“ sau „Gauss integrală“
- limită
- Pentru orice număr complex z următoarele ecuații sunt adevărate:
- Numărul e descompus într-o fracție continuă infinit, după cum urmează: adică,

- Sau echivalent:

- Pentru un calcul rapid al unui număr mare de caractere este mai convenabil de a folosi o altă descompunere:
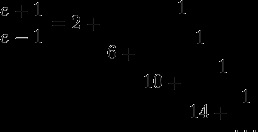
- Prezentarea catalană.
- Prezentare de produs.
- După un număr de Bell
- Măsura iraționalitate e egal cu 2 (care este cea mai mică valoare posibilă pentru numerele iraționale). [2]
Istoricul [modifică]
Aceeași constantă pentru prima dată calculat matematicianul elvețian Bernoulli în cursul rezolvării problemei de a limita valoarea veniturilor din dobânzi. El a constatat că în cazul în care suma inițială de $ 1 se plătește 100% pe an, o dată la sfârșitul anului, suma totală va fi de $ sau 2. Dar, în cazul în care aceeași sarcină dobânzii de două ori pe an, este de 1 $ înmulțit cu 1,5 de două ori, rezultând $ 1.00 × 1.5² = $ 2.25. Interes conduce trimestrial până la $ 1.00 x 1.25 = 2.44140625 $ 4, și așa mai departe. Bernoulli a arătat că, dacă rata dobânzii crește pe termen nelimitat, veniturile din dobânzi, în cazul dobânzii compuse are o limită. iar această limită este egală cu 2,71828 ...
$ 1,00 × (1 + 1/12) = 12 ... $ 2,613035
$ 1,00 × (1 + 1/365) 365 = $ 2,714568 ...
Astfel, e este un venit constant maxim net la 100%, iar frecvența maximă de capitalizare [3].
Prima cunoscută utilizarea constantă, în cazul în care este desemnat prin litera b. găsit în scrierile lui Huygens Leibniz. 1690 -1691 ani.
De ce e scrisoarea a fost aleasă. este necunoscut. Poate că acest lucru se datorează faptului că aceasta începe cu cuvântul exponențială ( „demonstrație“, „exponențială“). O altă ipoteză este că litera a. b. c și d sunt deja utilizate pe scară largă destul pentru alte scopuri, și e a fost primul „liber“ scrisoarea. De asemenea, este demn de remarcat faptul că e scrisoarea este primul nume în Euler (Euler).
Apropierea [citare]
Probleme deschise [modifică]
- Nu se cunoaște dacă numărul de perioade ale elementului inelar.
- Nu se știe dacă numărul de algebric independente.
- măsură necunoscută iraționalitate pentru oricare dintre următoarele numere: Pentru nici unul dintre ei nici măcar nu știu dacă este un număr rațional, irațional algebrice și numărul transcendental. [6] [7] [8] [9] [10] [11] [12]
- Nu se cunoaște dacă primul număr întreg Schiusa.