1. În alb caseta 2 și 4 bila neagră. Unul câte unul eliminat toate bilele în ea. Găsiți probabilitatea ca ultima minge este negru.
Notăm: A - un eveniment care constă în faptul că ultima minge trase dintr-o cutie - neagră.
Probabilitatea testului constă în faptul că acesta din urmă este recuperat minge - negru, este, probabil, cel mai frecvent test este de a extrage din sertarul de minge:
Apoi, acest test are 6 rezultate la fel de probabil :.
Dintre acestea eveniment elementar un rezultat favorabil.
Apoi, folosind definiția clasică a probabilității, avem:
- probabilitatea ca acesta din urmă a recuperat mingea va fi negru.
2. Lotul, format din 30 de straturi pentru bărbați, există 20 de produse fabricate pe plan local. Marfa selectează aleatoriu trei elemente. Care este probabilitatea ca toate cele trei produse vor fi:
a) producția locală; b) nu este produsă la nivel local.
a) Probabilitatea ca 3 dintre elementele selectate, toate cele trei vor fi produse la nivel local,
găsim următoarea formulă:
- numărul de metode de a elimina 3 elemente de producție locale din 20 (acest rezultat favorabil)
- - numărul de moduri în care puteți extrage 3 produse 30, (este toate rezultatele posibile).
Apoi. - probabilitatea ca cele 3 elementele selectate, toate cele trei vor fi produse la nivel local.
b) Probabilitatea ca 3 dintre elementele selectate, toate cele trei va fi nici o producție locală,
găsim următoarea formulă:
- numărul de moduri în care puteți extrage 3 produse sunt de producție nu locală de 30-20 = 10 (aceasta este un rezultat favorabil)
- - numărul de moduri în care puteți extrage 3 produse 30, (este toate rezultatele posibile).
Apoi. - probabilitatea ca cele 3 elementele selectate, toate cele trei va fi nici o producție locală.
3. Statistici cereri de împrumut în bancă este după cum urmează: 10% - agențiile de stat, 30% - alte bănci, altele - persoane fizice. Probabilitatea de credit default preluate după cum urmează: 0,01, 0,05 și 0,2. Găsiți probabilitatea de incapacitate de plată a noii cereri de împrumut. șef Departamentul de credit a raportat că mesajul este primit la implicit de împrumut, dar într-un mesaj de fax la numele clientului era ilizibilă. Care este probabilitatea ca împrumutul nu se întoarce nici o bancă?
Fie A denotă evenimentul „împrumutul nu este returnat“
H1 - creditul nu este returnat organismelor publice.
H2 - creditul nu este returnat orice bancă.
H3 - creditul nu este returnat persoanelor fizice.
Probabilităților H1 ipoteze. H2 și H3 în funcție de starea, sunt
probabilitatea condiționată a evenimentului A pentru aceste ipoteze, potrivit paribus
Apoi, vom folosi formula probabilității totale:
- probabilitatea de credit nu vor fi rambursate.
Probabilitatea ca împrumutul nu a returnat nici o bancă, vom găsi pe formula Bayes:
4. Care este probabilitatea de a obține cel puțin doi șesari cu trei aruncări de zaruri?
Fie A Notăm evenimentul „pe zar a scazut cu 6 puncte“
Probabilitatea acestui eveniment este determinată prin următoarea formulă:
, unde - numărul de rezultate la fel de posibile (pierderi 1,2,3,4,5 și 6 puncte). - numărul de rezultate favorabile (pierdere de 6 puncte).
Pierdere la trei aruncări de cel puțin două șesari înseamnă pierderea a două sau trei șesari.
Conform teoremei plus:
Pentru a găsi probabilitatea de a obține două și trei șesari cu trei aruncări de zaruri, se folosește formula Bernoulli
probabilitatea de evenimente de returnare:
Apoi: - probabilitatea de a avea cel puțin doi șesari cu trei aruncări de zaruri
5. Germinarea semințelor acestei plante este de 0,9. Găsiți probabilitatea ca din 900 de semințe plantate: a) încolțească exact 700; b) numărul de germinate cuprins între 790 și 830.
a) Găsiți probabilitatea ca exact 700 de semințe germina:
Noi folosim teorema locală Laplace:
și pot fi luate în considerare,
Ie probabilitatea unui eveniment, care a 900 de semințe plantate vor germina exact 700, este aproape de zero.
b) Găsiți probabilitatea ca numărul de semințe germinate se află între 790 și 830:
Cu condiția: - probabilitatea de germinare a semințelor,
Deoarece valorile și mari, folosim inegalitatea Cebîșev:
Probabilitatea ca o deviere a unei variabile aleatoare de așteptare matematică este mai mică decât unele număr:
simetrică Valoarea limită în ceea ce privește, prin urmare, de la inegalitate se poate trece la inegalitatea
Sau, comparati cu și pentru a obține:
Valoarea se măsoară prin formula:
6. Investitorul cumpără valori mobiliare pentru împrumutul luat de la rata dobânzii ipoteci r. Rata dobânzii pe X cu valori mobiliare - variabila aleatoare cu MX = a, o> r, DX =
a) folosind metoda de regresie, determină durata de pregătire necesară pentru un nou angajat la vârsta de 30 de ani.
Notăm - vârsta angajatului - timpul de pregătire
b) determinarea unui coeficient de corelație conform formulei:
- moment de corelare, caracterizat prin următoarea ecuație:
Așteptările și este definită ca:
Apoi, momentul de corelare:
Coeficientul de corelație este diferit de zero, prin urmare, valorile corelate.
9. Primirea primelor de asigurare în cele 130 de sucursale ale companiilor de asigurări din regiune A fost de 26 x 104 în. e. în regiune a reprezentat 18 · 104 din 100 de sucursale la. e. Valoarea de dispersie a primelor de asigurare în regiunea A este egală cu 39 x 108 (la. e.) 2. în regiune - 25 · 108 (. cu.) 2. La un nivel de semnificație a = 0,05, determina dacă valoarea medie semnificativ diferită a veniturilor primelor de asigurare în regiunile A și B, pe baza 1 ramură.
Prin ipoteză, se cunosc următoarele informații:
Pentru un anumit nivel de semnificație pentru a testa ipoteza nulă a egalității așteptărilor celor două populații distribuite în mod normal, este necesar să se calculeze valoarea observată a testului:
Și tabelul funcție Laplace pentru a găsi punctul critic al egalității
În cazul în care - nici un motiv pentru a respinge ipoteza nulă.
Dacă - respinge ipoteza nulă.
Noi definim mai întâi mediu și
Folosind tabelul Laplace pentru a determina punctul critic:
Și compararea. obținem:
Deci, nu există nici un motiv pentru a respinge ipoteza egalității așteptărilor distribuții de date.
Prin urmare, diferența de medii încasări ale primelor de asigurare în regiunile A și B, pe baza ramura 1 nu sunt esențiale.
Răspuns. aflux mediu brut al primelor de asigurare
Ele nu diferă în mod semnificativ
10. Compania de închiriere de mașini, interesat într-o relație între kilometraj de vehicule (A) și valoarea lunară de întreținere (Y). 15 masini au fost selectate pentru a determina natura acestei conexiuni.
Se trasează datele brute și determină natura dependenței pe acesta. Se calculează selectiv coeficientului de corelație Pearson liniară, verifică semnificația ei la = 0,05. Construiți o ecuație de regresie și să dea interpretarea rezultatelor.
Graficul de date brute:
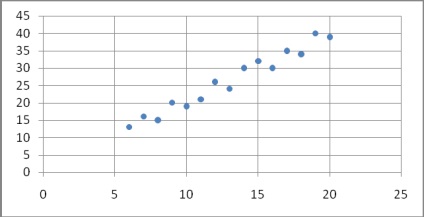
După cum se vede în graficul, relația dintre valorile X și Y pot fi luate ca liniar.
Coeficientul de corelație Pearson selectivă a liniară