Cinematica studiază mișcarea corpurilor, nu este interesat de motivele care contribuie la această mișcare.
Totalitatea corpului sau a organelor sistemului, adoptat convențional pentru poziția fixă relativă este determinată de alte organisme și dispozitivul de sincronizare (ceasuri sincronizate) este cadrul de referință spatio-temporala.
Pentru a putea studia mișcarea specifică a corpurilor, este necesar să se stabilească un anumit punct al corpului, primit de probă pentru un fix, care este, de a alege un așa-numitul punct de referință în raport cu care, și va fi poziția numărătoarea inversă a corpurilor în mișcare. Apoi, pentru a determina poziția corpului în raport cu originea necesității de a alege scara distanțelor de referință și instrucțiuni de ghidare ale raportului de poziție. Acest obicei folosesc trei axe perpendiculare între ele ale coordonatelor carteziene sau prin așa-numitele coordonate curbilinii generalizate, care includ polare, cilindrice și sistem de coordonate sferice. Adesea, alegerea sistemului de coordonate este definit de formulare a problemei. De exemplu, în studiul mișcării fluidului pe un tub cilindric convenabil sunt coordonate cilindrice, în cazul lichidului de curgere din sfera de cercetare sau gaz - sferic.
În cele din urmă, din moment ce mișcarea corpurilor se face în decursul timpului, pentru a descrie este necesar pentru a selecta timpul de referință și scara de timp.
Astfel, elementele cadrului de referință necesare pentru a descrie mișcările sunt: originea, amploarea distanțelor de referință, trei domenii de poziții de referință ale organismelor, timpul de referință, scara de timp.
Este evident că aceeași mișcare în cadre de referință diferite care se deplasează în raport unul cu altul, se va arata diferit. Astfel, viteza, accelerația, direcția și mișcare a traiectoriei de pasageri care se extinde din față spre partea din spate a mașinii, se deplasează rapid de-a lungul liniei de cale ferată curbată va fi diferită în cazul în care mișcarea luate în considerare în sistemele de referință asociate cu: a) transportul în mișcare; b) cu Pământul; c) soarele etc.
Ecuațiile cinematice ale mișcării
În cazul în care organismele de referință selectate ne-au conectat orice sistem de coordonate, mișcarea corpului poate fi studiată în ceea ce privește acest sistem de coordonate.
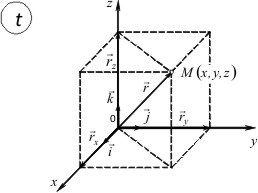
Pentru a determina poziția corpului în spațiul utilizat în mod normal de carteziene sistemul de coordonate x, y, z (fig. 1.1).
Poziția punctului M în raport cu sistemul de referință poate fi definit prin cele trei coordonate carteziene x, y, z reprezintă distanța de la acest punct la coordonate avioanele yz, zx, xy, respectiv.
Trei coordonate x, y, z pot fi combinate într-un segment de linie sau vector raza r direcționat, trase de la origine la punctul dat. Coordonatele x, y, z sunt proiecțiile pe axele și, prin urmare,
unde i, j, k - coordonează vectorii de unitate, adică versorii dirijate de-a lungul direcția pozitivă a axelor de coordonate x, y, z, respectiv, adică,
Geometric vector diagonal reprezentat paralelepipedului format prin trei vectori reciproc perpendiculare rx = xi, ry = yj, rz = zk și magnitudinea (valoare absolută) este egală cu
Vom folosi dreptul sistemului de coordonate, care se poate distinge între folosind regula de degetul mare. Înșurubarea sfredel drept buton filetat prin rotire în planul xy cel mai scurt drum de la capătul pozitiv axa x la capătul pozitiv al axei y, obținem traducerea degetului mare, care coincide cu direcția pozitivă a axei z.
Punct de circulație va fi descrisă în totalitate, dacă poziția sa va fi cunoscută în orice moment, în ceea ce privește cadrul de referință selectat.
Când mișcarea unui punct M de coordonata z, y, z și vector raza r t variază în timp. În mecanica, se consideră argumentul, adică variabilele independente, astfel încât să definească legea de mișcare a unui punct de material trebuie să specifice, fie sub formă de dependența funcțională a tuturor celor trei coordonate din când în când
sau dependența de timp a razei vectorului
Ecuațiile (1.3) și (1.4), se numește ecuațiile cinematice ale mișcării punctului material.
Locul geometric al tuturor punctelor de vectorul r raza numit M. traiectoria Ecuațiile de mișcare definesc traiectoria unui punct în formă parametrică. Rolul parametrului este timpul t. Dacă aveți nevoie pentru a obține ecuația traiectoriei ecuațiile cinematice ale mișcării elimină timpul obtinerea ecuația traiectoriei, care indică legătura dintre cele trei coordonate ale oricărui punct.