Conceptul de „câmp“ de studiu într-un curs de algebră mai mare.
Noi oferim o definiție mai precisă.
Câmpul este un set nevidă P, pe care sunt definite două operații algebrice binare, numite adăugare și multiplicare, 10 îndeplinesc următoarele axiome:
1.Pentru orice a, b, c, aparținând P, (a + b) + c = a + (b + c) - asociativitate plus;
2. Pentru orice a, b aparținând P, a + b = b + a - comutativitatea;
3. Există un element de zero, 0 aparținând P, că pentru orice element de o, deținută de P, are loc egalitatea: 0 + a = a + 0 = a - existența unui element de la zero;
4. Pentru orice element există un loc de muncă, care are loc egalitatea: a + (- a) = (- a) + a = 0 - pentru existența fiecărui element opus;
5. Pentru orice a, b, c, aparținând P, (a + b) * c = a * c + b * c, a * (b + c) = a * b + a * c - distributivitatea de multiplicare peste plus;
6. Pentru orice a, b, c, aparținând P, (a * b) * c = a * (b * c) - multiplicarea asociativitatea;
7. Pentru orice a, b aparținând P, a * b = b * o - multiplicarea este comutativ;
8.Suschestvuet element de identitate 1 aparținând P, care, pentru orice element o, deținută de P, egalitatea: 1 * a = a * 1 = a - existența unui singur element;
9.0 nu este egal cu 1. 0.1 P aparțin;
10.Dlya orice element a, nu este egal cu zero, există un invers 1 / a (un minus în primul grad), astfel încât ecuația: a * 1 / a = 1 / a * a = 1 - existența unui element invers pentru fiecare non-zero.
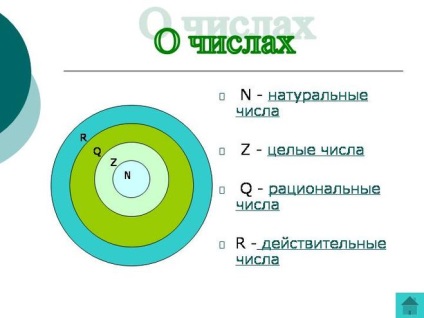
Din seturile de numere, care sunt studiate la școală (se arată în imagine) a câmpului sunt doar exemple ale setului de numere raționale și reale, din moment ce toate condițiile definiției câmpului. Un set de numere naturale (1,2,3.) Și numere întregi (. -3, -2, -1,0,1,2,3,4.) Nu formează un câmp, ca și pentru numerele naturale nu axiomele 3 , 4,9,10 (suficient pentru chiar și non-împlinire a unei axiomă 3, atunci nu se poate verifica), și numere întregi - axiomă 10.
Domeniul matematicii este utilizat în două moduri.
În primul rând, câmpul - este un set de obiecte pentru care operațiile de adunare, înmulțire și împărțire (cu excepția diviziunii obiect zero), cu astfel de obiecte, rezultatele acestor operațiuni sunt în cadrul setului. Din acest motiv, câmpul de numere întregi nu sunt: rezultatul operațiunii „1 împărțit la 2“, în mod evident, setul de numere întregi care nu aparțin. Aceasta stabilește o clasă numită „inel“.
Dar setul de numere raționale este un domeniu deja: prin împărțirea un număr de către o altă gestionare rațională rămâne un număr rațional.
În al doilea rând, câmpul - este. acest domeniu. Ceea ce am folosit pentru a apela câmpul din punct de vedere fizic. Cu un grad suficient de generalitate putem presupune că câmpul - este o funcție de mai multe variabile: dacă vom atribui o regulă prin care fiecare punct M i se atribuie o valoare de K (nu neapărat un număr par - acest lucru poate fi vectorul atât intensitatea câmpului electric și chiar tensor la fel ca în teoria generală a relativității), atunci avem, astfel, în spațiu, care aparțin punctul M, având în vedere un câmp.
Fie A - mult.
Definiție: A - câmp. dacă A - 1 inel comutativ (cu unitate), în care, pentru orice x ≠ 0 exista ---- ¹ H - un membru de retur, astfel încât: x · ---- ---- ¹ H = X- ˉ ------ ---- ---- ¹ · x = 1 ---
Acum vom înțelege că un astfel de inel este, inel comutativ și inel cu 1.
Def. A - inelul. În cazul în care două operațiuni sunt definite în A:
- Pentru orice x, y --- → A x + y A - plus;
- Pentru orice x, y --- → de la A x · y A - multiplicare;
astfel încât următoarele axiome:
- x + y = y + x;
- x + (y + z) = (x + y) + z;
- Există un (element de zero) 0 astfel încât x + 0 = 0 + x = x;
- Pentru orice x există (-x) astfel încât (-x) + x = 0;
- x (yz) = (xy) z;
- x (y + z) = xy + xz;
Def. A - când inelul A 1 - inel și există un (element de unitate) 1 astfel încât x = 1, · · x 1 = x.
Vă mulțumim! Și cum este folosit? Pot să vă dau un exemplu de un pic mai prietenos? 3 ani în urmă -
Ei bine, de exemplu, să ia mulțimea numerelor întregi Z. Să vedem, va fi un câmp sau nu? Prin ipoteză, dacă Z - câmp, ar trebui să fie inel comutativ inel și inelul 1 și au astfel un element de revenire pentru fiecare element al Z.
Bucurându-se de ..
Este inelul Z?
Da. Multiplicarea, plus prezent. Toate axiomele sunt îndeplinite.
Este Z un inel comutativ?
Deci, de asemenea, este. De exemplu, 3 = 5 * 3 * 5 = 15
Este inelul Z cu 1?
Da, este.
DAR Z nu este un domeniu, pentru că nu există nici un element invers pentru fiecare element al lui Z, pentru numere întregi. O celulă de revers - este 1 împărțită foarte acest element. De exemplu, un 3 și 1/3. Și a treia - nu este un număr întreg.
Dar o multitudine de numere iraționale (Q) și materialul (R), va fi câmpuri. Sortate acum? 3 ani în urmă -
Acesta este stabilit, în care toate numerele au o anumită proprietate. De exemplu, câmpul de numere întregi.
Este cunoscut faptul că operațiunile de adunare, scădere și înmulțire se realizează deasupra câmpului de întregi.
Acest lucru înseamnă că, dacă adăugați, scade sau multiplica două numere, veți obține un număr întreg.
O divizie - nu este definită. Se întâmplă că, prin împărțirea la o unitate la alta unitate, obținem rațional.
Prin urmare, toate cele patru operații aritmetice sunt efectuate pe domeniul numerelor raționale.
Nu contează cât vom adăuga, scădere, înmulțire și împărțirea numerelor raționale, vom obține din nou un mod rațional.
Sad Roger [170K]
Întregi nu formează câmpuri. Ele constituie o altă clasă de seturi - inel. 3 ani în urmă -
Da, poate. Nu sunt foarte bun la teoria câmpului în matematică.
Dar, de fapt, eu sunt încă dreptate. Câmp - este un set de numere care au o anumită proprietate. 3 ani în urmă -