a α, b α = A. Aa (proiect 2.1.2). Să presupunem că liniile a și b nu oblic, adică ele se intersectează. Apoi, există un β plane, care aparțin directe a și b. In acest plan β sunt drepte și un punct A. Deoarece linia și un punct A este determinată de planul său unic, atunci β = α. Dar b β și b α, prin urmare, β egal = α imposibilă.
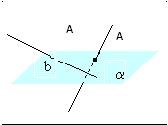
Două linii oblice au o perpendiculară comună, și este doar unul. Este comun perpendicular planuri paralele prin aceste linii.
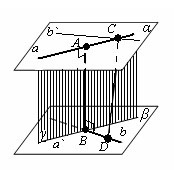
Fie a și b - date distorsiona linii. Prin ei paralel cu planul α și β. Drept care intersectează o linie dreaptă și perpendiculară pe planul a, într-un singur plan minciună (γ). Acest plan intersectează planul β a` dreaptă, paralelă cu. Fie B - a` punctul de intersecție al liniilor a și b. Apoi, linia AB, perpendicular pe planul α și perpendicular β plane, deoarece paralel β α. Segment AB - planuri perpendiculare comune a și β, și, prin urmare, o directă și b.
Vom dovedi că aceasta este singura perpendiculara comună. Să presupunem că liniile a și b, există un alt CD perpendicular comun. Trage o linie dreaptă prin B` punctul C, un b paralel. CD-line perpendicular pe linia B, o medie și B`. Deoarece este perpendicular pe linia A, este perpendicular pe planul α, și, prin urmare, paralelă cu linia AB. Se pare că prin liniile AB și CD, atât prin paralela pot fi trase avionul. În acest plan se va afla liniile noastre oblic AC și BD, ceea ce este imposibil, după cum este necesar.
Distanța dintre două linii oblice este lungimea comune perpendiculare.