Printr-un aranjament special cu consiliul editorial și editorial revista „Quantum“.
mișcare constantă
mișcare uniformă se numește mișcare în care punctul de material pentru orice intervale regulate, face aceeași mișcare. Ecuația forma vectorul de mișcare este scris ca:
în cazul în care - muta, - viteza, T - timp.
Propunerea unui punct este considerat întotdeauna în legătură cu orice organism, care, în această problemă este luată ca referință fixă, și se numește corpul. Acesta este asociat cu un sistem de coordonate; împreună cu corpul de referință formează un cadru de referință. Pentru mișcarea rectilinie este suficientă pentru a alege o axă de coordonate, de exemplu, OX. Apoi, poziția unui punct va fi determinat de coordonate x acesteia. Ecuația de mișcare uniformă într-o formă scalară va arăta astfel:
unde x0 - coordonarea unui punct în timp t = 0.
Alegerea corectă a cadrului de referință este adesea o soluție mult mai ușor la această problemă. Să luăm în considerare câteva sarcini specifice.
Problema 1. pasagerul din ferestrele de tren, venind la o viteză υ1 = 72 km / h, contorul vede trenul se deplasează cu o viteză υ2 = 31,4 km / h timp de 10 secunde. Se determină lungimea unui tren din sens opus.
Pentru corpul de referință va lua pasageri, iar axa de coordonate este îndreptată către o viteză a trenului din sens opus. Valorile υ1 υ2 viteze și specificate în raport cu un cadru fix de referință, de exemplu, pământ. În ceea ce privește același pasager, se deplasează cu o viteză de υ1. tren din sens opus este așa-numita viteză relativă υ2otn. care este egal cu
sau în formă scalară
Apoi, lungimea I dorită este egală cu trenul din sens opus
Zadacha2. Pescarul plutește pe o barcă până râu; care trece pe sub pod, el a scăzut în pălărie de paie de apă. O jumătate de oră mai târziu, el a găsit și se întoarse înapoi, prins pălăria, la 5 km sub pod. Care este viteza debitului râului, în cazul în care un pescar, se deplasează în sus și în jos pe râu, vîslit în același mod?
Noi asociem sistemul de referință cu apă în râu, care este cu o pălărie. Rybak scos din pălărie și abordări cu aceeași viteză, prin urmare, se prinde cu ea într-o jumătate de oră după pierderea detectată, sau o oră după pălăria care se încadrează în apă. În acest timp pălăria pe teren înotat 5 km. Deci, viteza debitului râului este egală cu 5 km / h.
Ravnoperemennoe mișcare liniară
Dacă viteza punctului material nu este constantă, dar în orice intervale regulate este schimbat la aceeași valoare, în acest caz vorbim de mișcare uniform accelerată. Numita mișcare uniform accelerată, dacă viteza crește și ravnozamedlennym dacă scade rata.
Pentru a rezolva problemele de pe acest subiect suficient să se știe ecuațiile pentru viteză și deplasare. ele sunt scrise în formă scalară după cum urmează:
Acolo υ0 - x0 inițial punctul vitezei - inițiale de coordonate și - accelerația, υ și x - viteza și poziția punctului în timpul t. Valorile υ0. a. υ și x va fi considerată ca fiind pozitiv atunci când direcția lor coincide cu direcția pozitivă a axei selectate de coordonate OX. negativ - în caz contrar.
Pentru a începe soluția este utilă cu o scurtă înregistrare a stării sale cât mai complet posibil sarcina traducerii în limba de simboluri. În același timp, trebuie să ne asigurăm că unitățile de toate dimensiunile au fost date în aceleași unități. Toate calculele sunt efectuate cel mai bine într-un mod general, adică, într-o denumire scrisoare, iar valorile numerice sunt substituite în rezultatul final.
Să ne rezolve următoarele probleme.
Problema 3. Două biciclist vor întâlni reciproc, unul dintre ele având o viteză de 5,4 km / h coboară de pe munte cu o accelerație de 0,2 m / s 2; de altă parte, cu viteza de 18 kilometri pe oră, accelerație în sus - 20 cm / sec 2. Cât timp vor întâlni?
Să presupunem că originea coincide cu poziția de start a primului călăreț, și direcția pozitivă a axelor de coordonate - cu direcția vitezei sale inițiale. Apoi condițiile stenografice ale problemei ar arata astfel:
υ01 = 5,4 km / h = 1,5 m / s
υ02 = -18 kilometri pe oră = -5 m / s
Scriem ecuațiile de mișcare pentru fiecare biciclist:
în care a1 = a2 cu condiția. La momentul întâlnirii
Rezolvarea ecuațiile (1) - (3), obținem
La această soluție ar putea încheia, dar în acest caz trebuie să vă asigurați că răspunsul primit are o semnificație fizică. Pentru a găsi această a doua rată de motociclist după 30 de secunde de la începutul mișcării:
= -5 m / s ± 0,2 m / s 2 • 30 = 1 m / s.
Se pare că al doilea ciclist în acest timp se va rula în jos de pe munte, nu de a urca pe munte. Evident, această sarcină este făcută incorect.
Sarcina 4. Balonul se ridică de la sol vertical cu o accelerație de 2,45 m / s 2. După 8 secunde de la începutul mișcării nacelei cade subiect. Cât de repede și cât de repede obiectul cade la pământ? rezistența aerului neglijat.
Deoarece primul obiect se deplasează cu balonul, apoi prin t1 = 8, se ridică la o anumită înălțime h1 și va avea o viteză care υ1
Deplasarea în continuare a subiectului poate fi descrisă în moduri diferite.
Adesea, acest tip de problemă rezolvată în două etape. În primul rând, obiectul este considerat mișcare lentă până la înălțimea maximă, apoi - cădere liberă la pământ. Provocarea, cu toate acestea, este ușor de rezolvat, dacă presupunem că un obiect în același timp implicat în două mișcări independente reciproc: ea uniform cu creșteri υ1 de viteză și cade liber. Cadru de referință asociat cu solul, iar axa de coordonate este îndreptată în sus. Apoi, ecuația de mișcare a unui obiect de la înălțimea h1 la sol poate fi scrisă ca:
(T2 - subiectul mișcării). Substituind în această ecuație expresia pentru h1 și υ1. obținem
Problema 5. Corpul este turnat vertical, în sus, cu o anumită viteză inițială. Când a ajuns la cel mai înalt punct de pe înălțimea de ridicare h = 100 m deasupra solului, din același punct de pornire și cu aceeași viteză inițială aruncat al doilea corp. La ce înălțime se vor întâlni? Ceea ce ei vor avea viteza la momentul întâlnirii? Ce organisme elementare au fost aruncate în viteza? rezistența aerului neglijat.
Să ne gândim mai întâi câteva caracteristici ale mișcării corpului aruncat în sus. Această mișcare complexă este suma a două numere prime - mișcare uniformă și cădere liberă. În timpul apariției fiecare mișcare în mod independent unul față de celălalt și de corpul este ridicat sau coborât. Prin urmare, putem spune că trecerea corpului aceeași porțiune din drum în sus și în jos, la fel și că viteza corpului la o anumită înălțime, atunci când se deplasează în sus sau în jos aceeași dimensiune.
Arată, de exemplu, că timpul de ridicare a corpului la înălțimea maximă de timp toamna este egală cu poziția inițială și viteza finală, care este egală cu cea mai mare viteza inițială. Să viteza inițială a corpului este υ0. Ecuațiile pentru viteza și coordonatele (punctul de origine asociat cu exprimate și axa de coordonate este orientată în sus):
La punctul de υ maxima de ridicare = 0, deci
Acum, corpul începe să cadă liber. Notăm timpul de scădere t“. și viteza de circulație finală υ „și scrie ecuațiile pentru cădere liberă
Acum, înapoi la problema noastră specială. Prin cele de mai sus, al doilea corp de ridicare la înălțimea h (fig. 1), egal cu căderea primului corp cu -h înălțimea H. este jumătate din timpul de cădere liberă a primului corp de la înălțimea H la sol, adică
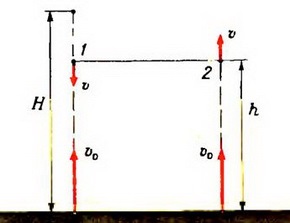
viteza corpului la momentul întâlnirii sunt egale în mărime și egală
În cele din urmă, considerăm problema în complotul.
Sarcina 6. este un grafic al vitezei a corpului față de timp (Fig. 2a). Construiți accelerare grafică, deplasare și calea.
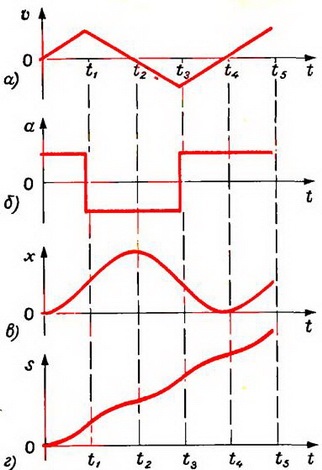
În primul rând, uita-te la modul în care corpul se mișcă la momente diferite. Din profilul vitezei arată că prima etapă (0 la t1) corpul se mișcă uniform accelerat; al doilea (de la t1 la t2) - ravnozamedlenno; a treia (de la t2 la t3) - accelerație uniformă, dar în sens invers; în a patra (de la t3 la t4) - ravnozamedlenno; în a cincea (de la t4 la t5) - .. uniform accelerat în direcția inițială și astfel graficele de accelerare de dependență, iar traiectoria timpului de deplasare sunt prezentate în figurile 2b, c și d, respectiv.
1. Pe două căi paralele într-o singură direcție sunt două trenuri: pasageri - 200 m lungime, la o viteză de 72 de km / h și prezentare - 400 m lungime, la o viteză de 45 km / h. Cât timp trenul de călători va trece un comerț?
2. Forțele coloanelor de închidere se întinde la 2,5 km și atingând o viteză de 5 km / h cu o notificare trimisă comandant motociclist, localizat în capul coloanei. Comandantul sa autosesizat și a scris răspunsul, în picioare pe marginea drumului, în. timp de trei minute. Pentru a determina viteza medie a călăreț dacă el a revenit la închidere după 9 minute 27 secunde.
3. Doi cicliști merge unul spre altul, una dintre ele având o viteză de 7,2 km / h coboară de pe munte cu o accelerație de 0,30 m / s 2; celălalt având o viteză de 36 km / h, accelerația este ridicat la 0,20 m / s 2. Care a fost distanța dintre bicicliști la momentul inițial, în cazul în care acestea sunt îndeplinite la 0,5 minute? La o lungime maximă a problemei de munte are o soluție?
4. Din moment ce corpul scade la o anumită înălțime. 2 cu aceeași înălțime de-al doilea corp scade. Câte secunde după începerea căderii primului corp pentru a dubla distanța ce separă corpul înainte de căderea celui de al doilea corp? rezistența aerului neglijat.
5. Elicopter se ridică la o viteză de 10 m / s. La o înălțime de 100 m este aruncat în sus din acesta obiect la o viteză de 2 m / s în raport cu elicopterul. Găsiți înălțimea maximă, care ajunge la subiect, precum și cât timp este nevoie și de cât de repede obiectul cade la pământ.
6. Organismul arunca în sus, la o viteză de 20 m / s. Care este înălțimea punctului, care organismul are loc de două ori, cu un interval de 3? rezistența aerului neglijat.
7. este un grafic al accelerației în timp (fig. 3). Se trasează cantitatea de deplasare a vitezei.