Distanța dintre două linii drepte paralele - este distanța de la un punct arbitrar al uneia dintre linii paralele la cealaltă linie.
Pentru a descrie grafic cele două linii paralele a si b observăm pe linie ca un punct arbitrar de M1, M1 picătură perpendicular dintr-un punct de pe linie dreaptă b, ceea ce denotă H1 ei. segment M1H1 corespunde distanței dintre liniile drepte paralele a și b.
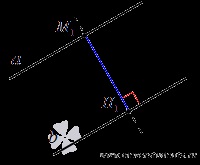
Această definiție a distanței dintre două linii paralele este valabilă pentru linii paralele pe un plan, și pentru spațiul tridimensional directe. Mai mult, o astfel de determinare a distanței dintre două linii paralele este acceptată de accident. Aceasta este strâns legată de următoarea teoremă.
Toate punctele de una din cele două linii paralele sunt îndepărtate la aceeași distanță față de cealaltă dreaptă.
Luați în considerare liniile drepte paralele a și b. Notă un punct de pe linia dreaptă M1 omite din acesta perpendicular pe linia b. Baza acestei perpendiculare este notată cu H1. Apoi M1H1 distanța perpendiculară este distanța dintre linii drepte paralele a și b, prin definiție. Vom dovedi că oricum. unde M2 - punct arbitrar directă a, un punct diferit de M1 și H2 - baza perpendicularei trasată de la punctul M2 pe linia b. Dovedirea acest fapt, și demonstrăm teorema în sine.
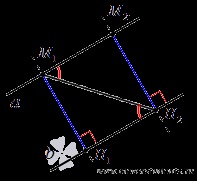
Deoarece unghiurile interioare în cruce situate formate prin intersecția a două linii paralele care se intersectează, sunt egale (acest lucru este discutat în articol linii paralele paralele cu linia), apoi. și direct M2H2, perpendicular linie b prin construcția liniei perpendiculare și. Apoi, triunghiuri M1H1H2 M2M1H2 și dreptunghiulare, și, în plus, ele sunt de-a lungul ipotenuzei și un unghi ascuțit: M1H2 - ipotenuzei comună. Din egalitatea de triunghiuri să fie egală cu laturile lor respective, așa. Acest lucru dovedește teorema.
Trebuie remarcat faptul că distanța dintre două linii paralele este cea mai mică dintre distanțele de la punctele de la o linie la celelalte puncte de linie.
Găsirea distanța dintre liniile paralele - teorie, exemple și soluții.
Astfel, găsirea distanței între liniile paralele este redusă la găsirea lungimii unei perpendiculara trase dintr-un punct de una dintre liniile de pe cealaltă linie. În acest caz, selectat o metodă pentru a găsi distanța. Alegerea metodei depinde de circumstanțele unei anumite sarcini. În unele cazuri, puteți utiliza teorema lui Pitagora, în altele - semnele de egalitate sau similaritate de triunghiuri, determina sinus, cosinus sau tangenta, etc. Dacă liniile paralele sunt date în sistem de coordonate cartezian, distanța dintre cele indicate linii paralele pot fi calculate prin coordonate. Pe ea și se va opri.
Formulăm condițiile problemei.
Să presupunem că avionul sau în spațiul tridimensional este un sistem de coordonate rectangular fix, având în vedere două linii drepte paralele a și b, și este necesar pentru a găsi distanța dintre aceste linii.
Soluția la această problemă se bazează pe determinarea distanței dintre liniile paralele - pentru a găsi distanța dintre două linii paralele date trebuie să:
determină coordonatele unui punct M1 situată pe linia a (directe sau b);
calculează distanța de la punctul M1 la linie dreaptă b (sau a).
Odată cu definiția M1 punct de coordonate pe oricare set de linii paralele, fără probleme, cu excepția cazului în desigur, știi principalele tipuri de ecuații directe pe plan și linia dreaptă în ecuația spațiu. Pentru a găsi distanța de la M1 până la punctul dorit al setului de linii paralele vor fi utile pentru informațiile pe care le de la secțiunea pentru a găsi distanța de la punctul de la linia.
În special, în cazul în care sistemul de coordonate dreptunghiular Oxy plan definește o ecuație linie dreaptă forma generală. și directă b, paralel cu linia a, - o ecuație generală a liniei. distanța dintre aceste linii paralele pot fi calculate prin formula.
Arătăm derivare a acestei formule.
Noi luăm punctul. care se află pe linia a, atunci coordonatele punctului M1 satisfac ecuația. adică, egalitatea. din care avem.
În cazul în care. apoi se dă ecuația normală a liniei b. și dacă. apoi se dă ecuația normală a liniei b. Apoi, atunci când distanța de la punctul de la linia b este calculată cu formula. și când - conform formulei

Aceasta este, pentru orice valoare a C2 distanta de la punctul de la linia b poate fi calculată conform formulei. Iar atunci când ia în considerare egalitatea. care a fost obținut mai sus, aceasta din urmă formula devine. La încheierea formulei de calcul a distanței dintre două linii paralele definite prin ecuațiile de tip directe general și este terminat.
Să ne rezolve exemple.
Pentru a începe cu găsirea distanței dintre două linii paralele definite într-un sistem de coordonate rectangular pe planul Oxy.
Găsiți distanța dintre liniile paralele și.
Este evident că linia care corespund ecuațiile parametrice ale liniei drepte pe planul vizualizare. Acesta trece prin punctul.
Distanța dorită dintre liniile paralele egale cu distanța de la un punct la o linie. Am calcula.
Noi obținem ecuația normală a unei linii drepte, ceea ce corespunde unei ecuații linie dreaptă a formei cu coeficientul unghiular. Pentru a face acest lucru, mai întâi vom scrie ecuația generală a liniei :. Acum, se calculează factorul de normalizare :. Multiplicarea că ambele părți ale acestei ecuații, avem o ecuație normală a unei linii :. Căutând o distanță egală cu valoarea modulului de expresie. calculat la. Astfel, distanța dintre liniile paralele este egală cu setul
A doua soluție.
Obținem ecuațiile generale stabilite de linii paralele.
Am constatat că linia corespunde ecuației generale a unei linii drepte. Vom trece din ecuația parametrică a tipului de linie la ecuația generală a acestei linii:

Coeficienții variabilelor x și y în ecuațiile generale derivate linii paralele sunt egale, deci putem aplica direct formula pentru a calcula distanța dintre liniile paralele pe planul :.
.