Încercați ca un operator să ia o proiecție. De exemplu, într-un plan paralel cu un vector. Chiar și doar o proiecție pe un plan paralel cu axa.
Eu încă nu înțeleg în cazul în care este câtul și unde kernel-ul. Vă rugăm să furnizați exemple și să indice în cazul în care există un spațiu câtul și în cazul în care nucleul. Ea poate veni la mine atunci.
Să nu.
Acordați-vă câteva exemple de functionalelor liniare din geometria, și vom ajuta cu nuclee (și cele Quotient groaznic)
norma euclidiană vectorilor tridimensionale.
Aici am citit în Kolmogorov (și în zeci de alte cărți). Aici este un pic tăiat.
Lăsați spațiul liniar și este un subspațiu. Două elemente și de echivalent în cazul în care diferența aparține acestora. Acest raport împarte toate clasele. Un element clasa de echivalență se numește coset (subspatiului). Colectarea tuturor acestor clase se numește spațiul câtul cu subspațiul.
Cred.
Ca exemple de tridimensionale subspatii pot cita: avionul, segmentele nu mai vine în minte (pot da mai multe exemple). Aici este pictat ca diferența dintre o singură pereche de vectori și diferența dintre cealaltă pereche de vectori se află în același plan (care este un trehmerki subspațiu):
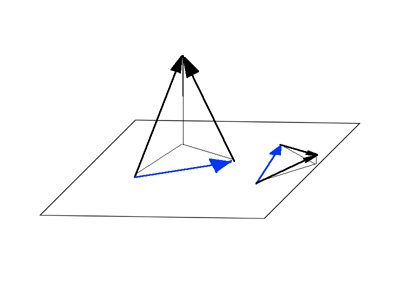
Există un vector, care este diferența în celelalte planuri. au vectorii de clasă pentru fiecare plan, diferența dintre care se află în ea. Atunci nu înțeleg în cazul în care spațiul câtul aici.
Acum funcțional (omite „liniar“ pentru concizie).
Noi numim set de nucleu set arbitrar de puncte ale sale, că există un număr pentru fiecare că, atunci când. Convex, din care miezul este non-gol, este numit un corp convex. În spațiu euclidian tridimensional, un cub, o sferă, un tetraedru sunt convexe corp.
De exemplu, un cub în spațiu tridimensional, spațiu -Trei-dimensional -ORAȘUL cub. - în cazul general, punctul de spațiu tridimensional, care nu este necesar să fie în interiorul sau la limita cubului, dar poate fi în afara ei. Ce este, eu nu pot imagina.
Segment - nu chiar un subspațiu. Și avionul - nu toate.
Direct la subiect. Suma a doi vectori pe linia se va afla pe o linie dreaptă, vector scalat va sta, de asemenea, pe o linie dreaptă. Același lucru pentru avion. În cazul în care acest lucru nu este un subspațiu, apoi a încălcat oricare dintre cele 8 proprietăți de plus și înmulțire cu un scalar?
Geometric convenabil să se presupună că vectorii sunt reprezentate grafic pe un punct fix. Apoi, capetele lor descriu unele subset de puncte. Care va corespunde cu un subset al subspațiile?
Planul care trece prin punctul fix?
miezul unei astfel funcționale (proiecție) - vectori axe ortogonale,
Firește. Ie respectiv. avionul.
Și în cazul în care cubul - kernel-ul, nu înțelege?