produs Vector dat coordonatele produs mixt

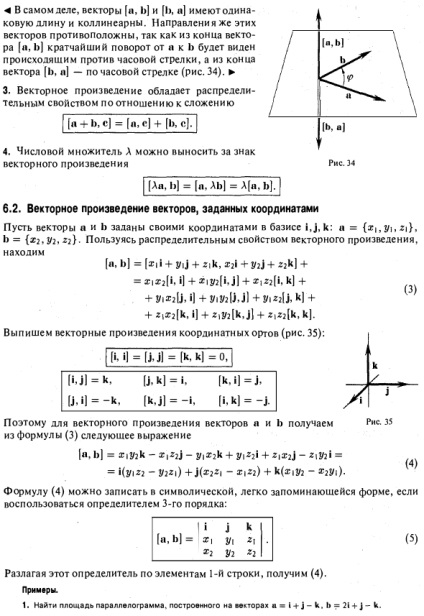




Definiția. Produsul vectorial al unui vector și un vector b este vectorul, notat cu simbolul [“, b] (sau L x L) astfel încât 1) lungimea vectorului [a, b] este (p, unde - unghiul dintre vectorii a și b ( Fig.31); 2) vectorul [a, b) perpendicular pe vectorii a și b, respectiv. perpendicular pe planul acestor vectori; 3) vectorul [a, b] este direcționat astfel încât de la capătul cel mai scurt rotație vector de la a la b se observă produce invers acelor de ceasornic (fig. 32). Fig. 32 Fig.31 Cu alte cuvinte, vectorii a, b, și [a, b) formează un vector dreptaci, adică poziționat ca degetul mare, arătător și degetul mijlociu de la mâna dreaptă. Dacă vectorii a și b sunt coliniari, vom presupune că [a, b] = 0. Prin definiție, lungimea produsului vectorial este numeric egală cu suprafața Sa paralelogramului (Figura 33.) Construit pe vectorii multiplicați a și b ambele părți: 6.1 . Proprietățile produsului vectorului 1. Produsul cruce este egal cu tolkotogda vectorul zero dacă și când cel puțin unul dintre vectorii tirajate este zero sau când acești vectori sunt coliniari (dacă vectorii a și b sunt coliniari, unghiul dintre ele este fie 0 sau 7d). Este ușor pentru a obține de la faptul că, dacă presupunem vector de la zero kollinsarnym orice vector, atunci starea de coliniaritate a vectorilor a și b pot fi exprimate ca 2. anticommutative produs vectorial, T. E. întotdeauna. Într-adevăr, vectorii (a, b), și [li, «] au aceeași lungime și sunt coliniari. Aceeași direcție acestor vectori sunt opuse, deoarece capătul vectorului [a, b] cel mai scurt rotația de la a la b va fi vizibil loc invers acelor de ceasornic, iar capătul vectorului [b, a] - sensul acelor de ceasornic (fig. 34). 3. Produsul vectorial are o proprietate de distribuție în ceea ce privește adăugarea 4. Un factor numeric poate fi luat ca semn al produsului vectorial 6.2. Vector produs coordonatele date Lăsați vectori a și b sunt date prin coordonatele sale în baza. Folosind proprietatea distributiv a produsului vectorial, vom găsi produsul vectorial al vectorilor de coordonatele date. Produsul amestecat. Să scrie produsul vectorial al coordonatelor vectorilor unitare (Figura 35.) Prin urmare, produsul vectorial al a și b sunt obținute din formula (3), cu următoarea formulă de expresie (4) poate fi scrisă în mod simbolic, ușor memorabil, dacă folosim determinantul treilea ordin: Extinderea determinant de elementele primul rând, obținem (4). Exemple. 1. Găsiți aria paralelogramului construit pe zona de vectori de căutare, prin urmare, în cazul în care vom găsi = 2. Găsiți aria unui triunghi (fig. 36). Este clar că zona b'd triunghi egală cu jumătate din suprafața S a paralelogramului Despre AU B. Calcularea produsului transversală (a, b | vectorilor a = OA și b = Ob, obținem Notă Produsul eco nu este asociativ, că egalitatea (. (a, b), c) = [a, | b, c)), în cazul general, nu este adevărat. De exemplu, atunci când a = ss j au § 7. Produsul mixt al vectorilor Să presupunem că avem trei vectori a, b și c. Inmultiti vectorii a și 1> vsktorno. Rezultatul este vectorul [a, 1>]. Înmulțim cu vectorul de la (a b), c). Numărul ([a, b], f) se numește produsul mixt al vectorilor a și b. c și notate (a, 1), e). 7.1. Sensul geometric al produsului mixt Amână vectorii a, b și c otobshey punctul O (fig. 37). Dacă toate cele patru puncte O, A, B, C află într-un plan (vectorii a, b și c sunt numite în acest caz coplanare), produsul mixt ([a, b], s) = 0. Acest lucru rezultă din faptul că vector [a, b | perpendicular pe planul în care se află vectorii a și 1“, și, prin urmare, vectorul cu. / Dacă punctul O, A, B și C nu se află într-un singur COSV-os (vectorii a, b și non-coplanar), se va baza pe marginile OA, OB și OC-o cutie (fig. 38 a). Prin definiție, produsul cruce au (a, b) = Deci, de unde Deci - zona paralelogram OADB și cu - un vector unitate perpendicular pe vectorii a și b, astfel încât triplu a, b, c - dreapta, adică, vectorii a, b și c sunt dispuse, respectiv, ca degetul mare, arătător și degetul mijlociu al mâinii drepte (Fig. 38 b). Înmulțind ambele părți ale acestei ecuații pe dreapta de vectorul pentru a obține că produsul vectorial dat coordonate. Produsul amestecat. Numărul de CSG cu aceeași înălțime h paralelipiped construit, luat cu semnul „+“ atunci când unghiul dintre vectorii s și cu o acută (tripla a, b, c - dreapta), și cu semnul „-“ atunci când unghiul - obtuz (triplu, b, c - stânga), astfel încât în acest fel, produsul mixt al vectorilor a, b și c este egal cu volumul V al paralelipipedului construit pe acești vectori ca coaste, în cazul în triplu a, b, c - dreapta, și -V, și dacă triplu , b, c - stânga. Bazat pe sensul geometric al produsului mixt, se poate concluziona că, prin înmulțirea tf vectorii a, b și c în orice altă ordine, vom primi întotdeauna 7 sau -K. Sign proiz- Fig. 38 conduită va depinde numai pentru că unele trei formează vectorii tirajate - dreapta sau la stânga. În cazul în care vectorii a, b, c formează un dreptaci, atunci drepturile vor, de asemenea, b triplu, c, a și c, a, b. În același timp, toate cele trei triplează b, a, c; a, c, b și c, b, a - stânga. Astfel, (a, b, c) = (b, a) = (c, a, b) = - (b, a, c) = - (a, c, b) = - (a, b precum). Esheraz subliniază faptul că produsul mixt al vectorilor este egal nulyutogdai numai atunci când vectorii multiplicată a, b și c sunt coplanare: 7.2. Produsul mixt al vectorilor în coordonate Fie a, b și c sunt date prin coordonatele sale în baza i, j, k: a = b = z2>, c =. Să ne găsim o expresie pentru produsul lor mixt (a, b, c). Am amestecat produs de vectori în baza zadannyhsvoimi i coordonatele, J, k, este egal cu determinant al treilea ordin, care linia desenată, respectiv, de la coordonatele unui prim, al doilea și al treilea vectori deînmulțitul. O condiție necesară și suficientă pentru coplanaritate a vectorilor în \, Z |>, b = c = poate fi scrisă sub forma U | z, az2 y2 = 0 -2. EXEMPLUL Uț. Verificați dacă vectorii „coplanari = b = c =. vectori contemplate vor fi coplanare sau non-coplanare în funcție, va fi egală cu zero, sau nu determinant al elementelor sale expansiune a primei linii, obținem D = 7- 6- 4- 15 + 6-3 = 0 ^ - n vectori, b, c sunt coplanare. 7.3. Double produs vector produs cruce [a, [b, c]] este vectorul perpendicular pe vectorii a și [b, c]. Prin urmare, se află în planul vectorilor b și c, și pot fi descompuse de către acești vectori. [! A, [> s]] Putem să arătăm că avem formula = L (a, e) - cu (a, b). Exerciții 1. Cele trei vectori AB = c, F? = O = b și CA sunt laturile unui triunghi. Exprimat în termeni de vectori, b și c, cu medianele AM coincizând, DN, triunghi CP. 2. Ce condiții trebuie să fie asociate vectorilor p și q, vectorul p + q partajat unghiul dintre ele în jumătate? Se presupune că toți cei trei vectori sunt legate la început de ansamblu. 3. Se calculează lungimea diagonalei paralelogramului construit pe vectorii a = 5p + 2q și b = p - 3q, dacă știți că | p | = 2v / 2 | q | 3 = H- (p7ci) = f. 4. Notând cu o și partea b a rombului se extinde de la un nod comun, dovedesc că diagonala rombului sunt reciproc perpendiculare. 5. Se calculează produsul scalar al vectorilor a = 4i + 7j + 3k și b = 31 - 5j + k. 6. Localizați a0 vectorul unitate, vectori paraleli a =. 7. Găsiți proiecția vectorului a = l + j- vector Kha b = 21 - j - 3k. 8. Găsiți cosinusul unghiului dintre vectorii IS «f, în cazul în care A (-4,0,4), B (-1,6,7), C (1,10.9). 9. Găsiți un vector unitate p °, ambele perpendiculare și vector = Ox. 10. Se calculează sinusul unghiului dintre diagonalele parallelofamma format prin vectorii a = 2i + J-k, b = i-3j + k ambele părți. Calculați înălțimea h a paralelipipedului format de vectorii a = 31 + 2j - 5k, b = j + j- 4knc = i-3j + k, dacă sunt luate din baza paralelogramului format de vectorii a și I). Răspunsuri