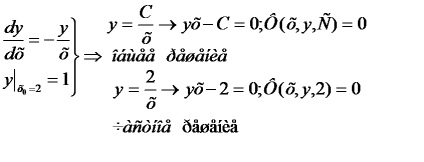Dacă ecuația () conține numai prima derivată a funcției dorite, această primă ecuație diferențială. Cea mai frecventă prima ecuație diferențială este de forma
În cazul în care este o anumită funcție continuă a trei argumente ale sale: în special, nu poate depinde de x sau y, dar trebuie să conțină în mod necesar.
Dacă ecuația (7.6) definește ca o funcție implicită a celorlalte două argumente, poate fi reprezentat sub forma rezolvată în ceea ce privește
Există o funcție continuă definită de x și y.
Ecuația diferențială (7.16) sau (7.17) x este variabila independentă în funcția dorită.
Primul Opredelenie7.4 ecuație diferențială este o relație care se referă funcția dorită, variabilele independente și prima derivată a funcției dorite.
DEFINIȚIE 7. 5 Decizia primei ecuații diferențială este orice funcție. care fiind înlocuit în ecuația (7.16) sau (7.17) se transformă într-o identitate.
Pentru ecuația diferențială (7.17), teorema următoare, numită teorema existenței.
Teorema 7.1 în ecuația (7.17) este continuă și derivatul său parțial este continuu într-o regiune care cuprinde un punct. există o soluție unică a ecuației
,
Semnificația geometrică a teoremei zaklyuaetsya că există unul și numai o funcționalitate este. grafic care trece prin punctul.
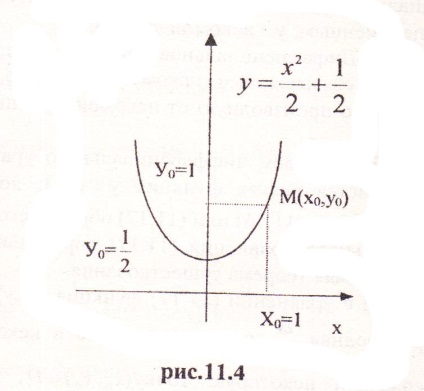
Exemplul 7.7: Să considerăm problema
În cazul în care este o funcție continuă și domeniul acestei funcții este mulțimea tuturor.
Ușor văzut. și anume, starea teoremei. Soluția acestei ecuații este
Determinată cu condiția ca la. adică. unde C = 1/2.
Stare. că, atunci când x = x0 functia y trebuie sa fie egal cu numărul de inițial y0 presetat. Se numește condiția inițială. Acesta este adesea scris sub forma
Definiție 7.6 Soluția generală a primei ecuații diferențială este o funcție. care variază de la o constantă arbitrară C, și îndeplinește următoarele condiții:
A) satisface ecuația diferențială pentru orice valoare particulară a constantei C C
B), indiferent de starea inițială, atunci când este posibil să se găsească o valoare C = C0 care satisface condiția inițială dată.
Aceste toate condițiile sunt îndeplinite, atunci și numai atunci, când starea teoremei de existență și unicitate.
În procesul de găsire a unei soluții generale a ecuației diferențiale, am ajuns adesea la relația dintre forma
Nu este permis în ceea ce privește y. permițând raportul în raport cu y, obținem soluția generală.
Cu toate acestea, exprimă y în ceea ce privește raportul (7.19) nu este întotdeauna posibil în funcții elementare. În acest caz, soluția generală a ecuației diferențiale este implicit.
. specifică implicit soluția totală, a numit-o ecuație diferențială comună integral.
Definiție 7.7: O soluție particulară este orice funcție. în cazul în care acesta din urmă arbitrar constantă C pentru a da o anumită valoare C = C0.
raportul numit particular ecuație integrală.