Teorema pe centrul unui poligon regulat >>
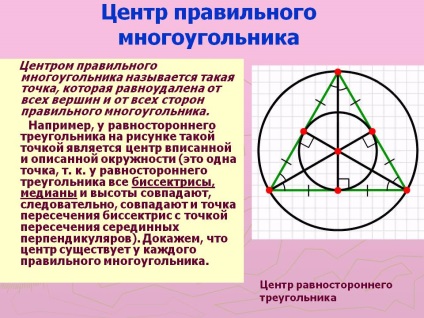
Centrul de poligon regulat. Centrul unui poligon regulat este numit un punct echidistant față de toate vârfurile și toate laturile unui poligon regulat. De exemplu, un triunghi echilateral în figură este un punct central al cercului inscris si circumscris (acesta este un punct, t. K. Toate au triunghi echilateral bisectoarea, mediana și aceeași înălțime, coincide deci cu punctul de intersecție al Bisectors midperpendiculars punctului de intersecție). Demonstrăm că există la fiecare poligon regulat. Centrul unui triunghi echilateral.
Slide 5 din prezentarea „Regular poligoane Geometrie“. dimensiunea arhiva cu prezentarea de 1454 KB.
Geometrie Grad 9
„Forme Symmetry“ - simetrie în jurul punctului. A` este punctul simetric cu punctul A linie l. Simetria în limba greacă înseamnă proporționalitate. Transformarea mișcării inverse, este de asemenea o mișcare. A. Există o linie si un punct A care nu se află pe o linie dreaptă. Ideea generală a cifrelor de conversie. Finalizat: Pantyukov EA M1. Există mai multe tipuri diferite de simetrie.
„Vector Rezolvarea problemelor“ - Utilizarea vectorilor pentru a rezolva problemele (partea 1). Tiviakov LA Exprimă vectorii AM, DA, CA, MB, CD prin vectorul a și vectorul b. № 3 Dan romburi ABCD. BE. CE = 3. 1. K - mijlocul DC. Grad 9. № 1 vectori de soare exprima, CD-uri, AC, OC, OA vectorilor a și b. № 2 vectori exprimă DP, DM, AC a vectorilor a și b.
„Mișcarea geometrie Grad 9“ - Rotire. transfer paralel. Atunci când segmentul de conducere este afișat pe segmentul. Simetria centrală. Mișcarea. Axial. Suprapunere. simetrie axială. Tipuri de mișcări. Conceptul de mișcare. Central. Teorema. simetrie axială a simetriei centrale Turn de transport paralel. Centrală și de simetrie axială. Orice mișcare este o superpoziție. Geometrie Grad 9.
„Geometrie poligoane regulate“ - centrul unui poligon regulat. Ia oricare trei noduri ale A1A2 poligon. O, cum ar fi A1, A2, A3. poligon regulat. Lecții de geometrie în clasa a 9-a. Figura prezintă un pentagon regulat, hexagon octogon. Demonstrăm că există la fiecare poligon regulat. Despre orice poligon regulat poate fi descrisă printr-un cerc, și numai unul.
"Cercul Grad 9" - O (xo, yo) - centrul cercului, A (x, y) - punct al cercului. № completați tabelul 1 următoarele date: Ecuația circumferința. Sarcini. Grad 9. Să d - distanța de la punctul de centru cerc la un plan prestabilit, R - raza cercului. 2. № 2 Derivarea ecuația unui cerc cu centrul la M (-3; 4) trecând prin origine.
Doar pe „Geometrie Grad 9 '54 prezentari