Fluxul de evenimente numite simplu (sau staționare Poisson), în cazul în care are doar trei proprietăți: staționare, și nu ordinară aftereffects. Numele de „simplu“, datorită faptului că procesele asociate cu fluxurile elementare, sunt cele mai simple descriere matematică. Cel mai simplu, la prima vedere, fluxul regulat nu este „ierta“, deoarece are o aftereffect: momentul apariției asociate dependenței funcționale rigide astfel fluxul de eveniment. Fără eforturi speciale pentru a menține regularitatea unui astfel de flux nu este creat de obicei.
Cel mai simplu fluxul joacă un rol special printre celelalte fire. Și anume, la cerere (superpoziție) a unui număr suficient de mare de fluxuri independente, staționare și obișnuite (comparabile între ele în intensitate) se obține prin flux aproape cele mai simple.
Pentru un simplu flux de interval de intensitate l între evenimentele adiacente este așa-numitul exponențială distribuției (exponențială) cu densitate
în cazul în care l - parametru de lege exponențială
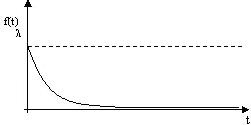
Fig. 1.9.2 Calendarul distribuției densității de distribuție exponențială
Pentru o variabilă aleatoare T având o distribuție exponențială, așteptarea este reciproca MT a parametrului, iar deviația standard egală cu valoarea medie a ST:
Teoria probabilității ca o „măsură de dezordine“ valoare aleatoare non-negativ este adesea considerat un coeficient de variație așa-numitele:
Din formulele (2), (3) rezultă că pentru NT exponențială de distribuție = 1, t. E. Pentru fluxul de evenimente mai simple coeficient de variație a intervalelor dintre evenimente este unitatea.
Evident, pentru fluxul regulat de evenimente, în care intervalul dintre evenimentele care nu este deloc întâmplătoare (nt = 0), coeficientul de variație este zero. Pentru majoritatea evenimentelor de curgere care apar în practică, coeficientul de variație al intervalelor dintre evenimente este cuprins între zero și unu, și poate servi ca o măsură a „gradul de regularitate“ debit: nt mai aproape de zero, fluxul de „obișnuit“. Simplu curs de apa - un „mai puțin regulate“ de la care apar în fluxurile de practică.
În calculele asociate cu fluxul de evenimente, este foarte convenabil de a folosi termenul de „elementul de probabilitate.“ Luați în considerare pe axa timpului cu un simplu intensitate de curgere l și elementar porțiunea poziționată în mod arbitrar (foarte mic) de timp Dt.
Elemente de probabilitate este probabilitatea de a obține de la acest interval de cel puțin un flux de evenimente. Este ușor de demonstrat că probabilitatea elementului (în afară de cantități mici de ordin mai mare decât Dt) egal cu:
t. e. pentru un simplu element de probabilitate flux egal cu debitul înmulțit cu lungimea intervalului elementar. Elemente de probabilitate, din cauza lipsei de efect secundar, nu depinde de cât de multe evenimente și atunci când au existat anterior.