Rețeaua cristalină poate fi determinată kaksovokupnost periodic puncte distanțate în spațiu, care sunt asociate cu centrele care formează un cristal de atomi sau molecule (Figura 4.2). Punctele la care sunt atomi sau molecule situate ei înșiși (mai precis, punctul despre care se executa oscilații de căldură) nazyvayutuzlami zăbrele (Figura 4.2, a). Grupul de atomi, care este asociat cu fiecare nod al grilajului (figura 4.2, b) nazyvaetsyabazisom (aceste grupe trebuie să fie identice în compoziție, locație și orientare).
O multitudine de noduri cu zăbrele, care este de fapt - abstract puncte set zăbrele obrazuetprostranstvennuyu (Figura 4.2, a) cristal.
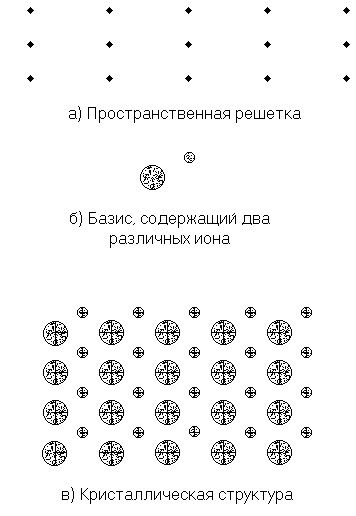
Astfel, rețeaua cristalină - un grilaj spațiu cu o bază.
Fig. 4.2. Structura cristalină: a) noduri cu zăbrele, care formează un spațiu cu zăbrele; b) un grup de atomi care este localizat la locurile cu zăbrele (baza); c) rețeaua cristalină, care este o „sumă“ a grilajului și a bazei; în această figură nodurile zăbrele nu mai este vizibil.
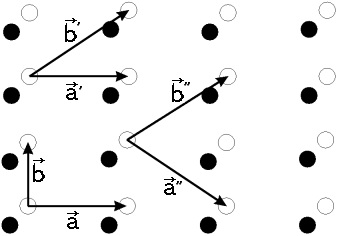
Fig. 4.3. Vectori emite un grilaj bidimensional cu o bază de doi atomi (alb și cerc negru). Alegerea acestor vectori este ambiguă (

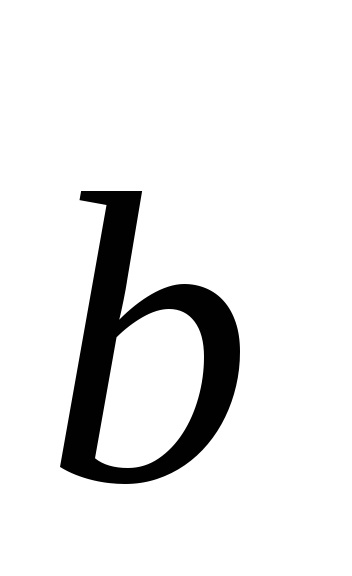

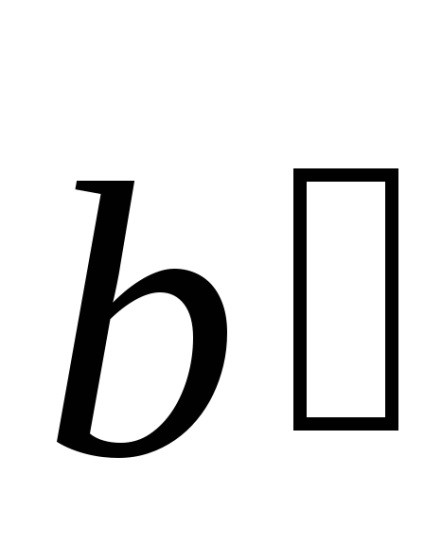



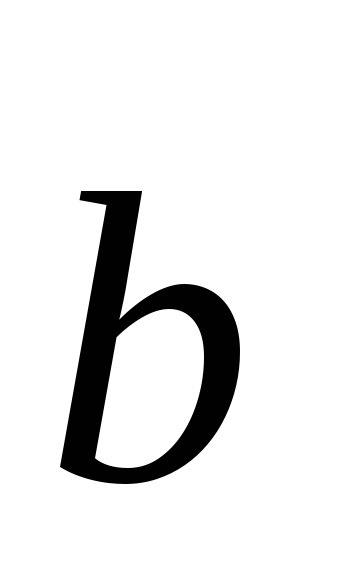

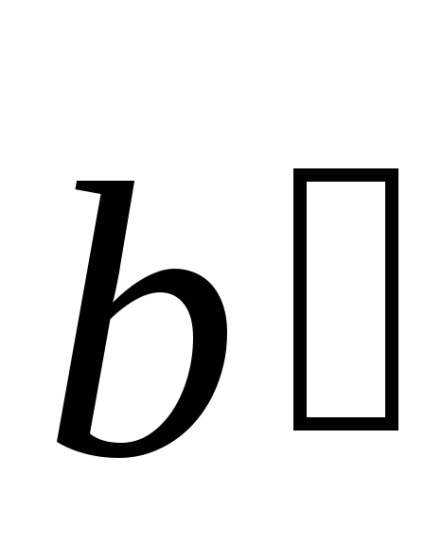


Noțiunea de grilaj spațiu a fost introdus de matematicianul francez și Cristalograful Auguste Bravais (1811-1863). Este deosebit de util dacă ne interesează doar periodicitatea spațială în aranjamentul atomilor în cristal, dar nu este interesat în compoziția sa chimică specifică. Pentru orice rețea Bravais (datorită frecvenței) nu pot găsi trei vectori situată într-un singur plan

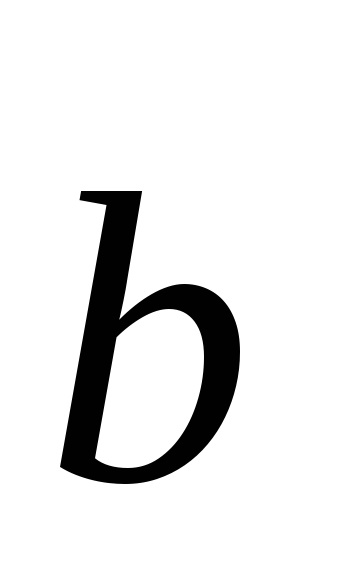
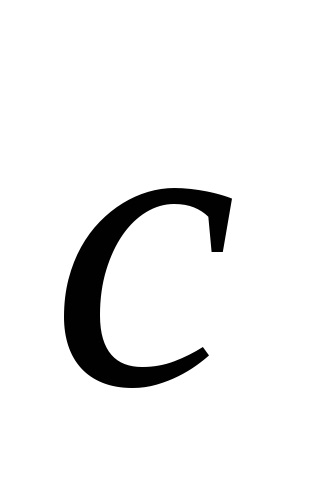
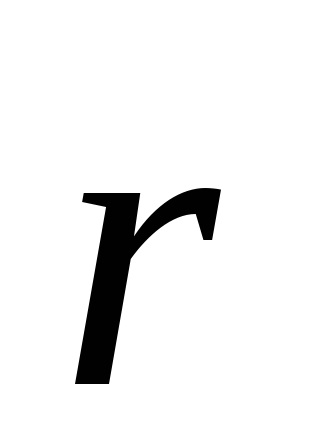
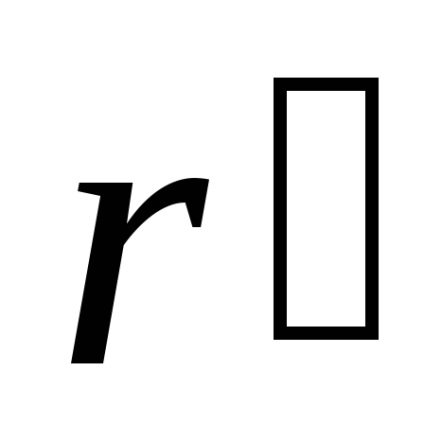
,
în care m, n ip - numere întregi arbitrare.
Astfel, toate punctele (noduri) Bravais zabrele echivalent ,. E. Au același mediu. Cu alte cuvinte, fiecare nod este vizibil din același model cu zăbrele.
vectori

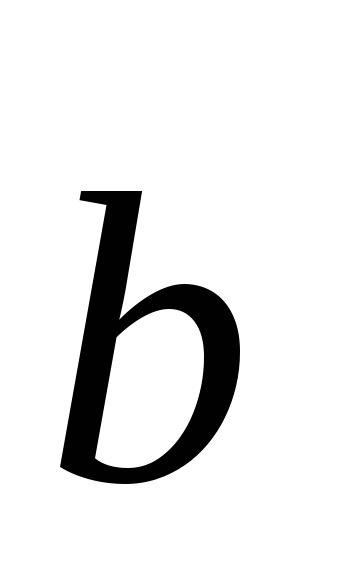
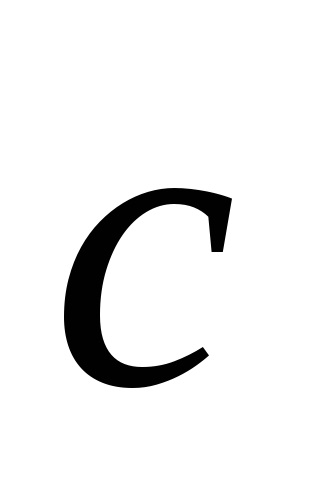
Este clar că vectorii

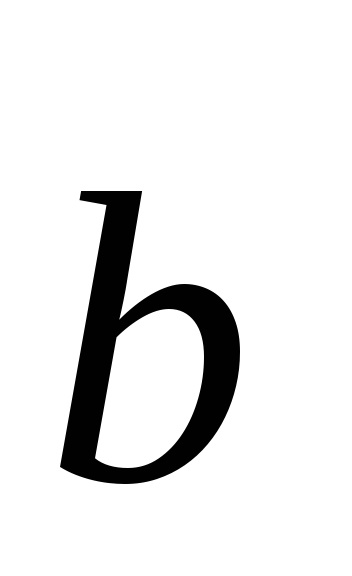
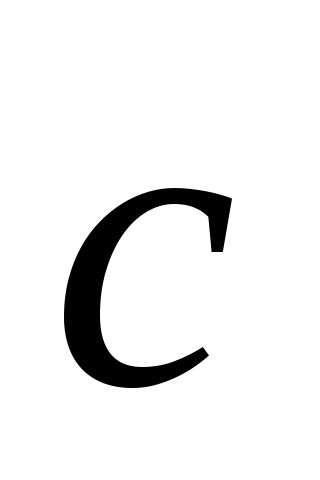

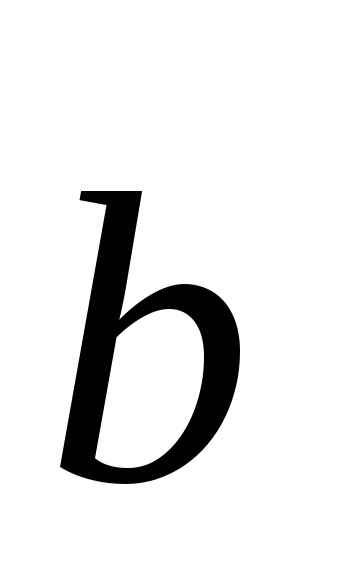
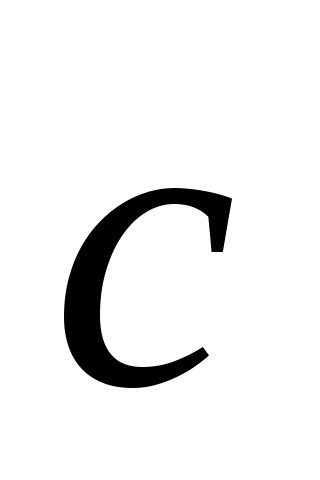
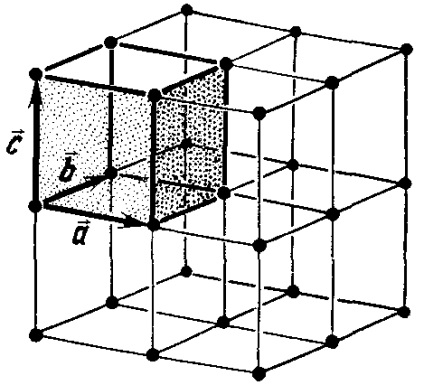
Fig. 4.4. Vectorii de traducere de bază

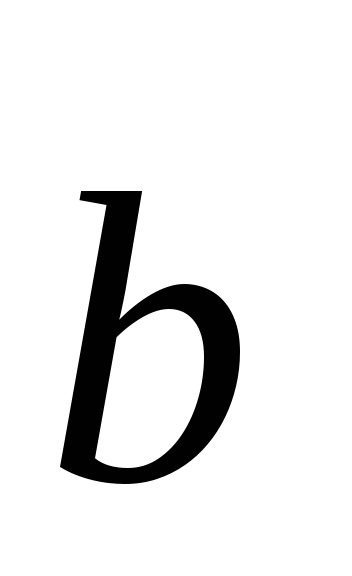
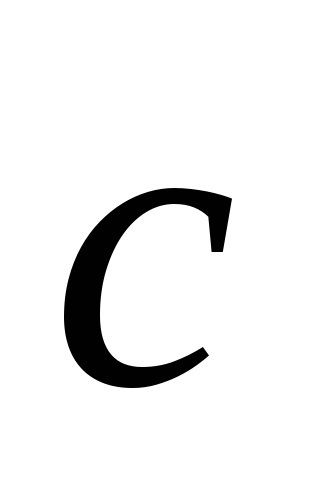
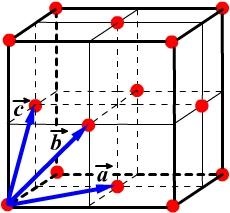
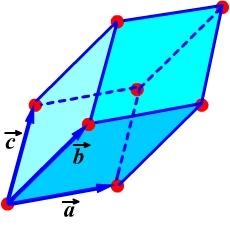
Fig. 4.5. Unitatea (a) și primitiv (a) dimensional zăbrele celulei Bravais. Acesta descrie un cub (fcc) grilaj centrată pe față. În toate figurile vectorii

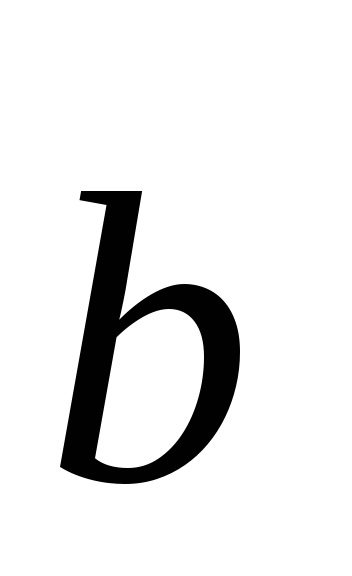
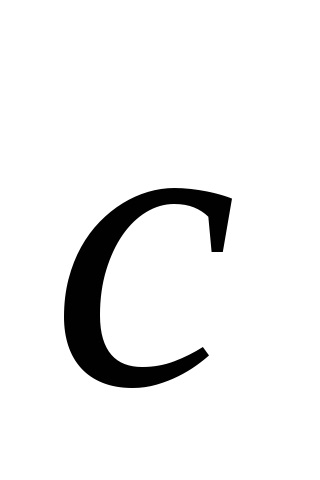
In celula primitivă are un singur punct al grilajului Bravais (Fig.4.5, c). In timp ce fiecare din cele opt colțuri ale paralelipipedului este un punct din rețea, fiecare astfel de punct aparține simultan opt celule, care sunt adiacente punctului luat în considerare, astfel încât o singură celulă are 81 / 8 = 1 punct. YacheykiVc volum primitiv definit de vectori de bază emisiuni de produse mixte:
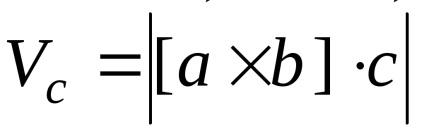
Celula primitivă este un caz special al celulei unitate. În acest caz, principalii vectori ai emisiunilor, și, prin urmare, celula primitivă, de asemenea, pot fi selectate în diferite moduri. Fig. 4.3, de exemplu, (

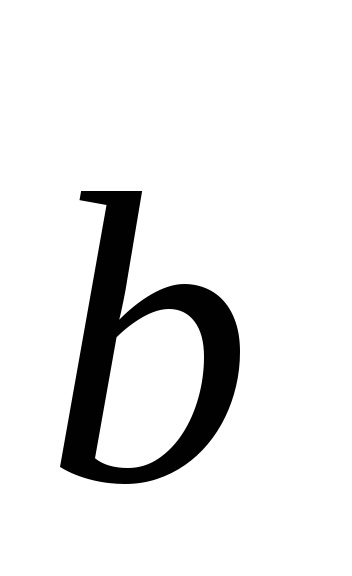

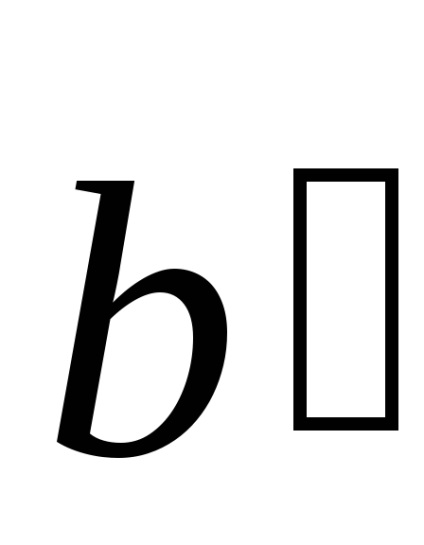


O altă opțiune este alegerea celulei primitive prezentată în Fig. 4.6. Celulele selectate în așa fel este numită în fizică celula primitivă Wigner-Seitz.
Pentru caracteristici unice ale unității selectate, sau celula primitivă (Fig.4.5, c), în general, trebuie să stabilească valori 6: 3 celule de margini a, b și uc trei unghiuri ele -, și . Aceste valori de celule nazyvayutparametrami. Lungimea laturilor celulei unitate, adică, lungimea emisiunilor vectorii de traducere de bază nazyvayutperiodami.
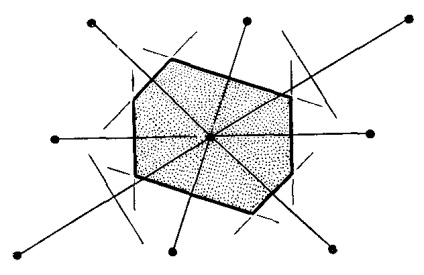
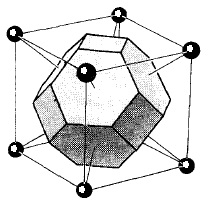
Fig. 4.6. Celulele primitive pot fi selectate după cum urmează: (a): 1) la liniile de legătură un punct dat zăbrele cu toate punctele adiacente; 2) prin mijlocul liniilor perpendiculare pe ele) dețin o nouă linie (în cazul unei latice bidimensională) sau plan (în cazul unui grilaj tridimensional. Celula astfel obținută este cel mai mic volum care conține doar un singur punct din rețea se numește o celulă primitivă Wigner-Seitz. Folosind astfel de celule pot umple întregul spațiu al rețelei cristaline precum și prin celulele primitive reprezentate în Fig. 4.3. Simetria primitiv Wigner-Seitz coincide cu Bravais zăbrele simetrie. Acest lucru poate fi văzut prin exemplul unei celule tridimensionale Vigenra Seitz (a) un CENTRU cubic (BCC) latice centrat pe corp (b).
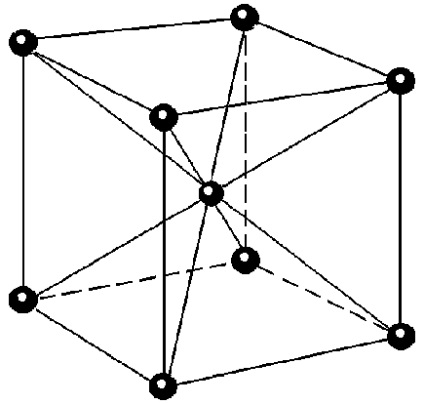
Prin intermediul traducerilor adecvate (schimburi) în vectorii de celule primitive

Cristalele multor metale si baze gaze inerte constă dintr-un singur atom. Dar structura anorganică și biochimice cunoscute, baza care include o mie sau mai mulți atomi.
Dacă baza de rețea cristalină constă dintr-un atom, rețeaua cristalină este simplu. În acest caz, toți atomii de cristal sunt aranjate într-un Bravais noduri cu zăbrele.
În cazul în care baza este formată din câțiva atomi, rețeaua cristalină este complexă. In acest caz, fiecare atom are propriile sale atomi podreshetkaodnotipnyh de bază, identică Bravais cristal cu zăbrele.
Un exemplu de un grilaj complex bidimensional prezentat în Fig. 4.3. „Alb“ și atomii „negre“ pot fi chimic identice, dar ele sunt diferite în poziția în rețeaua cristalină. Atomii unui cristal de același tip, dacă acestea sunt chimic identice și fiecare dintre ele este una vizibilă și aceeași imagine a rețelei cristaline.
Astfel, pentru a „vedea“ zăbrele Bravais, este necesar să se „vedea“ doar același tip de atomi. Când acest cristal cu un grilaj complex poate imagina două moduri: 1) ia o bază și difuzat în mod repetat utilizând vectori de traducere primitive, sau 2) iau mai multe Grile Bravais exact identice și includerea lor unul în celălalt, poziționate la nodurile tablourilor respective de aceiași atomi de tip . cristal bi-dimensional în Fig. 4.3, de exemplu, este format din două inserate unul în altul Grile Bravais, în care nodurile sunt aranjate respectiv „alb“ și „negre“ atomi.