2.2.5. Formula generală a lentilei.
suprafețe sferice sistem centrat se numește, în cazul în care centrele suprafețelor situată pe aceeași linie.
Raportul dintre suprafața sferică poate fi aplicată pe rând la toate suprafețele precum relația Lagrange-Helmholtz
Cel mai simplu centrat lentila subțire sistematic delimitată de suprafețe sferice, cu raze de curbură, și
Lentilele sunt biconvexe, plano-convexe, biconcave, plano-concav, concavo-convexe.
Colectarea de lentile se numește în cazul în raze paralele paraxial ale fasciculului după refracție se întâlnesc la un moment dat, iar împrăștierea dacă rezultatul cristalinului refracție într-un fascicul de raze paralele este transformată într-un fascicul de raze divergente.
Un obiectiv este considerat a fi subțire în cazul în care grosimea sa este mică în comparație cu raza de curbură și suprafețele de delimitare. În acest caz, vârfurile suprafețelor sferice îmbina în mod substanțial într-un singur punct O. numit centru optic al lentilei.
Orice linie care trece prin centrul optic al lentilei se numește axa optică. Axa optică, care coincide cu axa de simetrie a sistemului, numit principal, iar partea rămasă.
Orice rază paraxiale care trece prin centrul optic al lentilei nu experiență refracție.
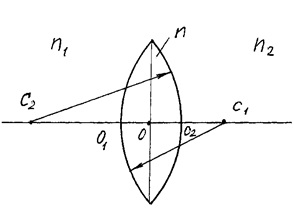
Luați în considerare o imagine punct sursă generată de lentila subțire, cu raze de curbură.
Scriem formula pentru suprafețe sferice
În cazul în care - d; n-refracție lentilă index, iar indicele de refracție al media înainte și după lentila.
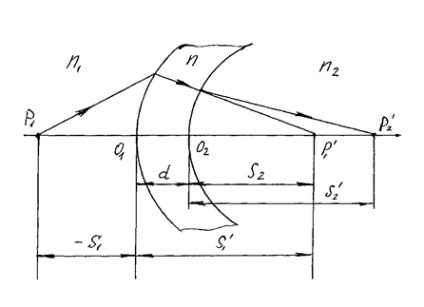
Pentru o lentilă subțire. Combinarea (1) și (2), se obține o formulă lentilă subțire
În cazul în care obiectivul este situat într-un mediu omogen,
Obținem o formulă sub forma unei lentile subțiri:
Notând - indice de refracție relativ al materialului lentilei în ceea ce privește mediul, obținem
2.2.6. puterea optică și distanța focală a obiectivului.
Ecuația sub forma unei lentile subțiri:
În cazul în care F puterea optică a unei lentile subțiri. Este egală cu suma puterilor optice ale suprafețelor sale sferice. Deoarece ecuația (6), este valabil pentru toate razele paraxial ale fasciculului, fasciculul homocentrică după refracție rămâne homocentrică și imaginea stigmatic este.
Pentru o lentilă, situată într-un mediu omogen cu indicele de refracție, puterea optică este determinată prin formula:
Pentru o lentilă subțire poate introduce conceptele de față și din spate și se concentrează principalele lungimi focale și i.
Lungimea focală din spate (8)
Distanța focală frontală (9)
Astfel: (10)
Dacă mediul în care este plasat lentila, aer, m = 1 și puterea optică a lentilei este legată de raportul de distanță focală:
În cazul în care pe ambele părți ale diferitelor medii ale cristalinului, atunci relația:
2.2.7. Formula lui Newton. Creșterea a cristalinului.
Ecuația lentilă subțire poate fi utilizat în continuare ca formula Newton
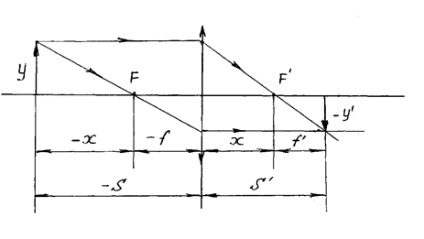
și în care - distanța față de obiectul și imaginea, măsurată de la focii principal.
Creșterea lentile este determinată de formulele.
2.2.8. Construirea imaginii în lentile.
Pentru a construi imaginea creată de o lentilă subțire, convenabil de a utiliza următoarele reguli care decurg din definițiile și rezultatele de bază (Fig. 3).
1.Luch care trece prin centrul optic al lentilei, situat într-un mediu omogen, nu refractate.
paralelă 2.Luch cu axa optică principală, după refractie trece prin lentila de focalizare principal din spate, în cazul în care obiectivul colectează și continuă fasciculul traversează lentila de focalizare principal, situat pe o parte a subiectului, în cazul în care obiectivul este divergente.
3.Luch care trece prin centrul principal de lentile după refracție este paralelă cu axa optică principală.
partea paralelă 4.Luch a axei optice, după refracție trece prin punctul focal partea din spate a obiectivului, în cazul în care obiectivul colectează și trece printr-o continuare a concentra partea din față în cazul în care dispersorul.
asista construcție grinzi pentru construcția cursului oricărei raze, după refracție într-o lentilă subțire, paralel cu aceasta, și care trece prin centrul optic. Punctul de intersecție al fasciculului auxiliar cu planul focal definește focalizarea lateral, în care toate grinzile transversale posibile, paralel cu aceasta.
1. Se obține o formulă lentilă subțire.
2. Cum este puterea optică a lentilei subțire?
3. Cum sunt lungimi focale de lentile subtiri?
4. Poate un lentile lenticulare care trebuie colectate?
misiune de muncă independentă.
Luați în considerare auto-imagistica in lentile subtiri la diferite poziții ale obiectului.
1. DV sivukhin Cursul general al Optica fizica: Proc. Alocație. - M. Science, 1985-725s.
2. Landsberg GS optică. - M. Science, 1976.
3. Savelyev IV Curs de fizica generala. T.2.M. Știința, 1988-478s.; V.3 1988-205s.
4. Boutique EI Optika.-M. Vyssh.shkola, 1986.-512S.
5. Kalitievsky NI Optica Wave. - M. Vyssh.shkola, 1978,383s.
sistem optic 2.3.Tsentrirovannaya.
2.3.1 Teoria Gauss pentru sistemul optic ideal.
Orice sistem optic este o colecție refractant centrată și suprafețe reflectorizante. Într-un ideal grinzi homocentricity sistem stocate optic și o imagine este similară cu geometrically subiectului, adică, fiecare punct, linie, plan în spațiul obiect punct de meci, linia, planul în spațiul de imagine. Teoria este centrată perfect sisteme optice a fost dezvoltat de Gauss în 1841. și este un caz special al problemei mai generale de transformare geometrică a unui spațiu la altul, ceea ce se numește transformare coliniare. Teoria gauss stabilește o serie de așa-numitele puncte cardinale și avioane, sarcina care descrie pe deplin proprietățile sistemului optic și vă permite să-l utilizați fără a ține cont cursul real al razelor în sistem.
Luați în considerare refracția pe o suprafață sferică.
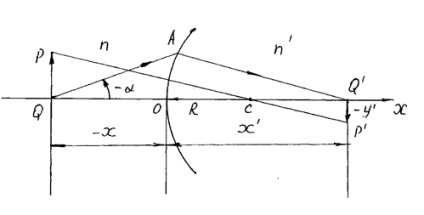
De la (1) și (2) se obțin prin conversia formulei
Formula (3) poate fi pus în baza teoriei geometrice a oricăror sisteme centrate în paraxial razele homocentrică. Prin aplicarea lor succesivă se poate obține locația imaginii finale date de întregul sistem. Aceste formule set corespondență coliniare între punctele de spațiu de obiect și puncte de spațiu imagine.
Din formulele de potrivire a coliniare următoarele proprietăți ale imaginilor optice în sistemele centrice.
1. Fiecare spațiu obiect plan este descris ca un avion
2. Fiecare linie descrisă ca o linie dreaptă la subiecții spațiu
3. Fiecare punct al spațiului obiect este reprezentat ca un punct în spațiu
2.3.2 plan și punctele cardinale.
Punctul principal al planului și un sistem optic.
Două avioane conjugate care apar între ele pentru a crește cruce
. Ei au numit planurile principale și
Punctele de intersecție ale planurilor principale cu axa optică principală, numită principalele puncte.
Poziția planele principale sunt definite prin raze de curbură a refractant și suprafețe de reflexie, distanțele dintre ele și indicii de refracție ai media delimitate de aceste suprafețe. Prin urmare, principalele avioane pot fi atât în interiorul cât și în exteriorul sistemului, atât pe aceeași parte a limitării suprafețelor sistemului, și pe ambele părți.
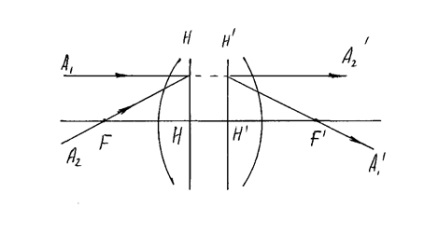
H -Front planului principal, -ORAȘUL planului principal posterior
plan focal și focalizare a sistemului optic.
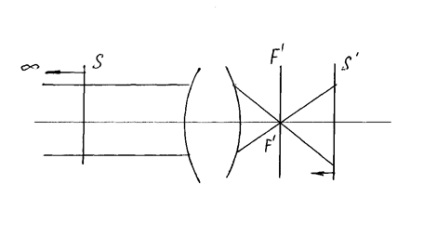
Planul focal spate este planul conjugat la infinit situat pe un plan în spațiu a obiectelor. perpendicular pe axa. Punctul de intersecție cu planul focal posterior al axei optice principale conferă poziția de focalizare din spate a sistemului (F ') (fig. 3).
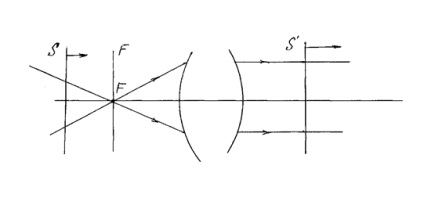
planul frontal focal este un conjugat plan la la infinit situat în imagini plane spațiu. perpendicular pe axa. Punctul de intersecție cu planul focal frontal al axei optice principale conferă poziția de focalizare frontală a sistemului (F) (Fig. 4).
punct nodal și planul
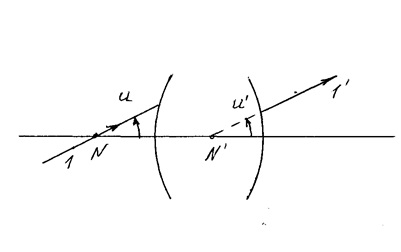
Nodul numit situată pe punctele conjugate pe axele optice N și având proprietatea care trece prin ele (sau de fapt, în interiorul extensiei imaginare a sistemului) grinzilor conjugate sunt paralele între ele (adică raportul de mărire unghiulară)
Plan perpendicular pe axa și care trece prin planul nodale sunt numite noduri. În cazul în care mass-media de pe ambele părți ale sistemului sunt aceleași, atunci punctele nodale coincid cu directorul.
2.3.3. Formula sistemului optic.
Pentru a construi imaginea centrată în sistemele ideale, puteți utiliza următoarele reguli:
1) Fasciculul care trece prin punctul central F, iese din sistem paralel cu axa optică în punctul specificat, astfel încât continuarea grinzilor de intrare și de ieșire se intersectează într-un punct aparținând planului principal H;
2) fasciculul incident paralel cu axa optică, la punctul de ieșire se execută astfel încât continuarea fasciculelor de intrare și ieșire se intersectează într-un punct care aparține planul principal din spate.
3) incident de fascicul, astfel încât extinderea acesteia intersectează punctul de ancorare N. dezautentifica paralel cu primire și extinderea acesteia intersectează axa optică la nodul.
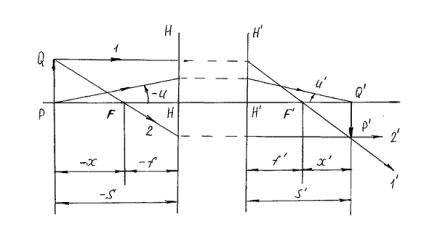
Relații de bază care caracterizează centrat sistem optic ideală, următoarele
Formula Newton (4)
Formula (5)
Lungimile focale sunt măsurate din planurile principale.
Puterea optică a sistemului este determinată prin formula:
Când F> 0, sistemul este numit de colectare, cu F<0 – рассеивающей
Lungimile focale sunt legate prin derivarea relația Lagrange-Helmholtz
2.3.4 sistem a crescut.
Sistemul creștere centrat poate fi obținută cu ajutorul formulei Lagrange-Helmholtz. și formulele care decurg din relațiile geometrice (Fig.6)