Text Lecții de decodare:
Știi deja două cazuri de dispunerea reciprocă a liniilor în spațiu:
Rechemare definițiile lor.
Definiția. Linii în spațiu numit intersectându dacă se află în același plan și au un punct comun
Definiția. Direct în spațiul numit paralel, dacă se află într-un singur plan și nu au puncte comune.

Comună tuturor acestor definiții este faptul că liniile se află în același plan.
Spatiul nu este intotdeauna asa. Putem face cu câteva avioane, și nu la fiecare două linii se vor afla în același plan.
De exemplu, muchiile cubului ABCDA1B1C1D1
AB și A1D1 află în planuri diferite.
Definiția. Două linii sunt numite oblic în cazul în care nu există nici un astfel de plan, care este folosit trecut prin aceste linii. Din definiția este clar că aceste linii nu se intersectează și nu sunt paralele.
Demonstrăm o teorema care exprimă un semn de linii oblice.
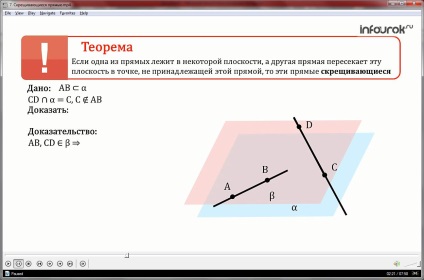
Teorema (semna linii oblice).
În cazul în care una dintre liniile se află într-un plan, iar cealaltă linie intersectează planul de la punctul nu face parte din această linie, atunci acestea oblic drept.
AB directă se află într-un plan α. Direct plan CD α intersectează într-un punct C, care nu aparțin liniei AB.
Dovedește că liniile AB și DC - sunt traversate.
Dovada este de contradicție.
Să presupunem că AB și CD-ul se află în același plan, vom nota cu β.
Apoi, planul β trece prin linia dreaptă AB și un punct C.
Prin corolarul axioma, de linia AB și situată pe punctul ei C poate fi făcută avionul, și, în plus, doar unul.
Dar avem deja un astfel de plan - planul a.
De aceea, p și avioane alfa coincid.

Dar acest lucru este imposibil, din moment ce CD-line intersectează α, și nu face parte din ea.
Avem o contradicție, deci, ipoteza noastră este falsă. AB și CD-ul se află în
avioane diferite și sunt oblic.
Deci, există trei modalități posibile de dispunere reciprocă a liniilor în spațiu:
A) liniile se intersectează, adică au doar un singur punct comun.
B) liniile sunt paralele, și anume, se află într-un singur plan și nu au puncte comune.
B) Intersectare directă, și anume nu se află într-un singur plan.
Luați în considerare o altă teoremă de linii oblice
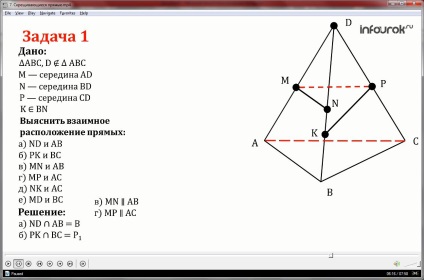
Teorema. Prin fiecare dintre cele două linii oblice se extinde un plan paralel cu o altă linie, și numai unul.
AB și CD - linii oblice
Dovedește că există un plan α astfel încât linia AB se află într-un plan α, iar linia de CD-ul paralel cu planul α.
Demonstram existența unui astfel de plan.
1) După punctul A desena o linie dreaptă paralelă AE CD.
2) Deoarece liniile AE și AB se intersectează, prin intermediul lor, puteți desena un avion. Notăm prin α.
3) Deoarece linia CD paralela AE, AE și α se află într-un plan, planul liniei CD ∥ α (prin teorema perpendicularitatea liniei și un avion).
Plane α - planul dorit.
Vom dovedi că avionul a - numai satisfacerea.
Orice alt plan care trece prin linia AB, va traversa AE, și, prin urmare, în paralel cu linia de CD-ul ei. Ie orice alt plan care trece prin AB intersectează linia de CD-ul, deci nu este o paralelă.
Prin urmare, planul α - numai. Acest lucru dovedește teorema.