Biot - Savart -. Laplace conductor care transportă un element de I. dl curent care creează un punct A (Figura 164) Câmpul de inducție dB. Este scris sub forma
unde dl - modulo vector egal cu dl lungimea elementului conductor și care coincide cu direcția curentului, r - vectorul rază,
elementul dl extras din conductorul la punctul A al câmpului, r - raza vectorilor modulus ra-dB direcție perpendiculară dl și r. t. e. perpendicular pe planul de co-Tora aparțin, și coincide cu o tangentă TION la liniile de inducție magnetică. Această direcție poate fi găsit prin găsirea liniile regulă de inducție magnetică-TION (regula șurub dreapta): direcția de rotație a capului dă direcția șurubului dB. dacă mișcarea de translație a șurubului corespunde direcției curentului în elementul.
unitate vector dB este determinată de tine, expresii
unde a - unghiul dintre dl și g
Pentru câmpul magnetic, ca și pentru electron-un izolator, principiu deține superpo-zitsii: câmp de inducție magnetică rezultantă-prezent creat mai multe atunci kami sau taxe în mișcare, este egală cu suma vectorială a inducției magnetice câmpurile comprimabile produse șoc kazh-fum sau încărcare se deplasează în de-similarity-:
Calculul caracteristicilor de câmp magnetic (V și H) în conformitate cu formulele prezentate în ob cazul de față este destul de complexă. Cu toate acestea, în cazul în care distribuția actuală are o anumită simetrie, utilizarea Biot - Savart - Laplace, împreună cu superpoziția Prince-POM face destul de simplu pentru a calcula domeniul specific. Ras-cautati două exemple.
1. Curent de câmp magnetic - curent care curge prin lungimea infinit pro directe a apei fine (Figura 165.). La un punct arbitrar A, conductorul îndepărtat de axa distanță R, vectorii dB din toate elementele actuale au direcție one kovoe perpendicular pe planul de desen ( „noi“). De aceea, adăugarea de vectori dB pot fi înlocuite prin adăugarea de modulele lor. Ca și în constanta de integrare alege unghiul a (unghiul dintre dl vectori și r), care exprimă toate cantitățile rămase prin acesta. Fig. 165 Rezultă că
(Raza CD arc se datorează micimea dl r, și unghiul de FDC pentru același motiv poate fi considerat direct). Substituind aceste expresii în (110,2), constatăm că inducția-mage magnetic creat de împăcării element de conductor este
Deoarece unghiul a pentru toate elementele de pe primele intervale de curent de la 0 la i, apoi în conformitate cu (110,3) și (110,4)
În consecință, câmpul magnetic de inducție de curent continuu
2. Câmpul magnetic în centrul conductorului circular cu un curent (Fig. 166). După cum rezultă din desen-se, toate elementele unui conductor circular cu curent creează un câmp magnetic în centrul aceeași direcție - de-a lungul normal de la bobina.
Prin urmare, vectorii de plus-set pot fi înlocuite prin adăugarea dB-em modulele lor. Deoarece toate elementele conductoare sunt perpendiculare pe vectorul rază (= 1 sina), iar elementele de distanță ale tuturor polițiștilor-circulare conductor de curent pentru a centra aceeași și egală cu R, atunci, în conformitate cu (110,2)
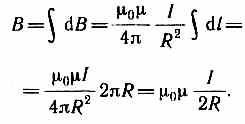
În consecință, câmpul de inducție magnetică în centrul conductorului circular cu curent
18. Fluxul câmpului magnetic. Teorema Gauss pentru # 7682;.
Flux de inducție magnetică (flux magnetic) printr-o zonă numită. cantitate scalară. unde unghiul dintre vectorii (vectorul normal la planul buclei) și.
Pentru un câmp uniform, și o suprafață plană perpendiculară pe vectorul. . Fluxul magnetic prin aria suprafeței este însumarea algebrică a debitului prin părți ale suprafeței.
Gauss' teorema: flux magnetic de inducție prin orice suprafață închisă este zero :.
Aceasta teorema reflectă absența tarifelor magnetice, prin care liniile de flux magnetic nu au nici început sau sfârșit și sunt închise.
19. Teorema privind circulația vectorului # 7682;, aplicarea sa la câmpurile de calcul. câmp electromagnetic.
Teorema de circulație în vectorul este în studiul câmpului magnetic aceeași valoare ca teorema Gauss în Electrostatica, deoarece permite să găsiți inducția câmpului magnetic, fără a aplica legea Biot-Savart Laplace.
1). Demonstrăm validitatea teoremei circulație vectorului În exemplul câmpului magnetic curent perpendicular pe planul figurii 1. și direcționată către noi (Fig. 13). Imaginează-un circuit închis, sub forma unui cerc cu raza r. La fiecare punct al vectorului de contur B este identic în magnitudine și direcționată tangențial pe circumferința. În consecință, circulația vectorului B este egal cu
Astfel, bazat pe vectorul V. circulație teorema am derivat o expresie pentru inducerea magnetică a câmpului curent continuu, derivat de mai sus (2.6).
2). Calculăm bobina de inducție magnetică în interiorul - o bobină cilindrică constând dintr-un număr mare de spire este uniform înfășurat pe un miez comun. Luați în considerare solenoid de lungime l. având n înfășurări prin care curentul (fig.14) curge. Lungimea solenoid cred că este de multe ori mai mare decât diametrul de spire sale, și anume, considerat solenoid infinit de mult. Studiul experimental al câmpului magnetic al solenoidului efectuate folosind pilitură de fier arată că câmpul din interiorul solenoidul este uniform, solenoidul este neuniformă și foarte slabă, adică, acesta poate fi considerat, practic, egal cu zero.
vector circulație în buclă închisă care coincide cu una dintre liniile de inducție magnetică ABCD. n și cuprinzând toate bobinele potrivit (9.2) este egal cu
Integrala peste ABCD poate fi reprezentat în două - porțiunea exterioară ABCD (este egal cu zero, deoarece solenoidul este B = 0) și DA internă.
La stația de DA circulație vectorul B este BL (contur coincide cu linia de inducție magnetică); Prin urmare,
Prin urmare, vom ajunge la o expresie pentru câmpul de inducție magnetică în interiorul solenoid (în vid)
S-a obținut, care este câmp uniform în interiorul solenoidului.
3). Esențial pentru practica câmpului magnetic are, de asemenea, un toroid - spire elicoidale inelare din care sunt înfășurate pe un miez având o formă torus. Câmpul magnetic este concentrat in interiorul toroid, este nici un câmp. Toroid poate fi privit ca solenoid suficient de mult timp înfășurat împreună într-un inel și folosind formula de calcul a intensității câmpului magnetic al toroid (10.2):
Mai mult, lungimea I a toroid trebuie luate în considerare în linia mediană, neglijând diferența mică dintre circumferințele exterioare și interioare ale inelului.
Ampere forță este forța cu care acționează câmpul magnetic de pe conductorul, un curent este plasat într-o cutie. Magnitudinea acestei forțe poate fi determinată prin legea lui Ampere. Această lege este determinată forța infinitezimal pentru o porțiune infinitezimală a conductorului. Ceea ce face posibilă aplicarea legii la conductorii de diferite forme.
Formula 1 - Legea lui Ampere
Magnetic de inducție B, în care conductorul parcurs de curent
Eu curentul în conductorul
dl elementul infinitezimal cu un conductor de curent de lungă
un unghi alpha între câmpul magnetic extern și direcția curentului în conductorul
Direcția forței Amperi este pe regula stanga. Formularea acestei reguli sună. Când mâna stângă este poziționat astfel încât liniile de inducție magnetică a câmpului extern sunt în palma și patru degete alungite indică direcția curentului de mișcare a conductorului, în care degetul mare este îndoit la un unghi drept pentru a indica direcția forței care acționează asupra elementului conductor.
Figura 1 - Regula mâna stângă
Mai multe probleme apar atunci când se utilizează regulile de mâna stângă, în cazul în care unghiul dintre câmp și curentul de inducție este mic. Este dificil să se determine care ar trebui să fie palma deschisă. Prin urmare, pentru ușurința aplicării acestei reguli pot fi plasate manual, astfel încât nu a fost parte a vectorului de inducție magnetică în sine, și amploarea acesteia.
Din legea lui Ampere, rezultă că forța Ampere este zero, atunci când unghiul dintre linia de inducție magnetică și curent de câmp este zero. Adică, conductorul va fi amplasat de-a lungul unei linii. Și Amperi forță va avea valoarea maximă posibilă pentru acest sistem, în cazul în care unghiul va fi de 90 de grade. Aceasta este, curentul va fi perpendicular pe linia de inducție magnetică.
Folosind legea lui Ampere poate fi găsit forța care acționează asupra sistemului de cei doi conductori. Imaginați-vă două conductoare infinit lungi, care sunt distanțate unul față de celălalt. Pentru acești conductori, fluxul de curenți. Forța exercitată de către câmpul produs de un conductor care transportă un număr de curent unu la numărul doi conductor poate fi reprezentat ca.