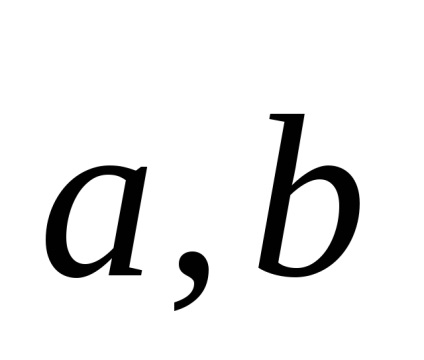Concepte de bază ale algebrei vectoriale
cantități scalar și vectoriale
fizica Desigur elementar este cunoscut faptul că anumite cantități fizice, cum ar fi temperatura, volumul, greutatea, densitatea, etc. determinată numai de o valoare numerică. Aceste cantități sunt numite valori scalare sau scalare.
Pentru a determina alte cantități, cum ar fi forța, viteza, accelerația și altele asemenea, în plus față de valorile numerice, trebuie să solicitați o alta și direcția lor în spațiu. Valorile care, în plus față de valoarea absolută este de asemenea caracterizată prin direcția numită vector.
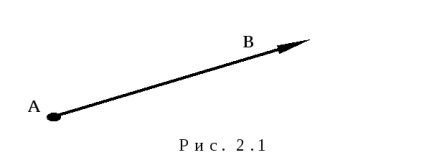
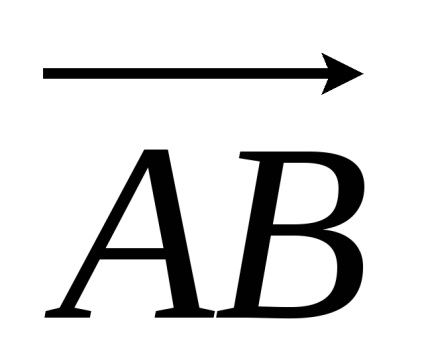
OpredelenieVektorom numit un segment direcționat, care este definit prin două puncte: primul punct definește începutul vectorului, iar al doilea - la sfârșitul anului. De aceea, se spune că un vector - o pereche ordonată de puncte.
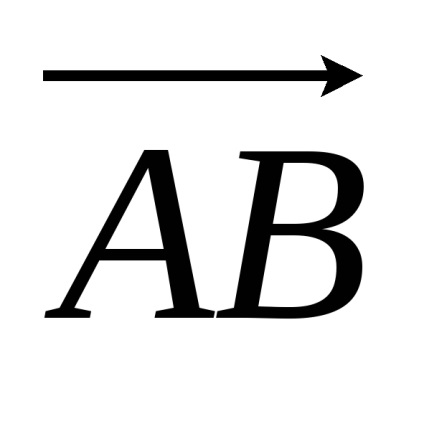
Cifra este reprezentată printr-un vector segment de linie în care direcția săgeții marcată de începutul vectorului la sfârșitul anului. De exemplu, Fig. 2.1.

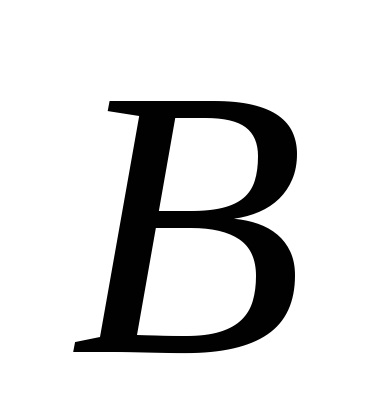

Prin vectori includ vectorul zero. a cărei început și sfârșit sunt aceleași. Este notat
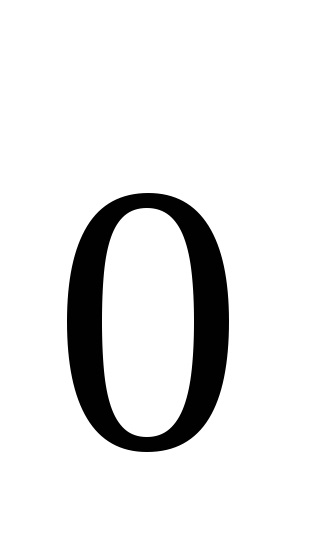
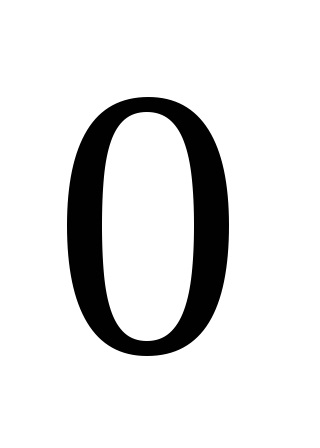
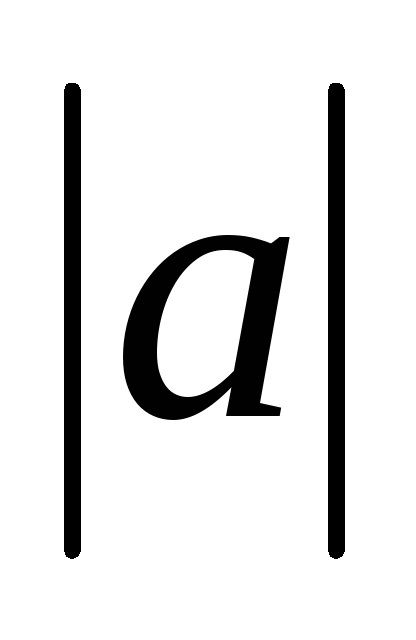
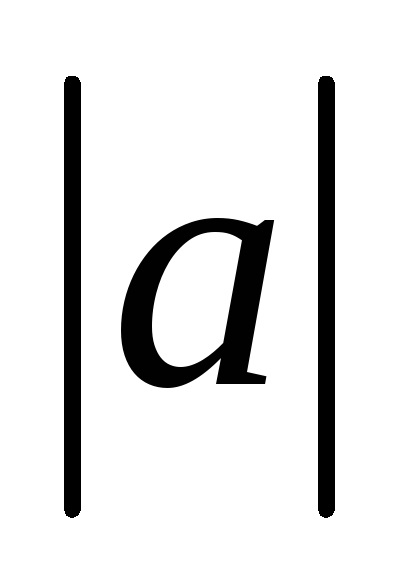
Distanța dintre începutul și sfârșitul vectorului se numește lungimea acestuia, sau modul. modul vector este indicat prin două bare verticale pe stânga:
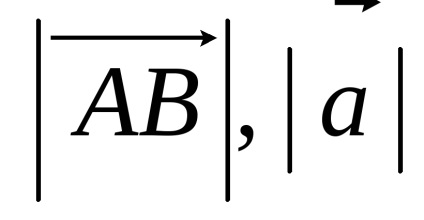

Vector paralel cu aceeași linie se numesc coliniare.
Vectori se află în același plan sau paralel cu același plan se numesc coplanari.
Zero vector este considerat a fi coliniare la orice vector. Lungimea sa este egală cu 0.
Definiție Doi vectori
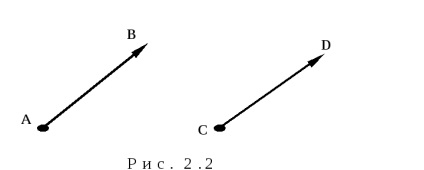
Acest lucru este scris ca:
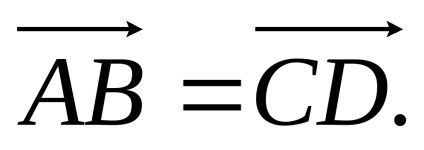
Din definiția egalității vectorilor rezultă că vectorul de transfer paralel este un vector, egal cu inițială, deoarece începutul vectorului poate fi plasat în orice punct al spațiului. Astfel de vectori (geometrie mecanică teoretică), dintre care la început pot fi plasate în orice punct în spațiu, numit liber. Și acestea sunt vectorii vom lua în considerare.
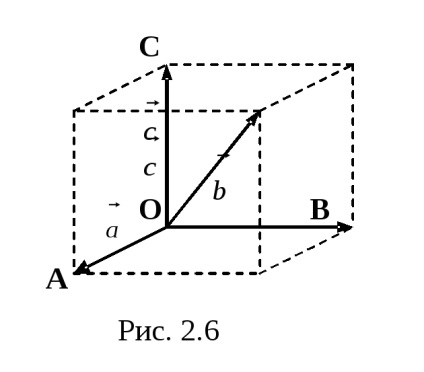
vectori OpredelenieSistema
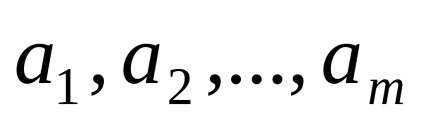
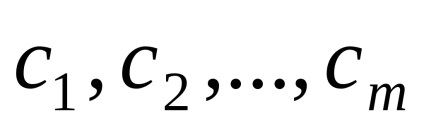
OpredelenieBazisom în spațiul menționat la arbitrare trei vectori necoplanare care sunt luate într-o secvență.
OpredelenieEsli
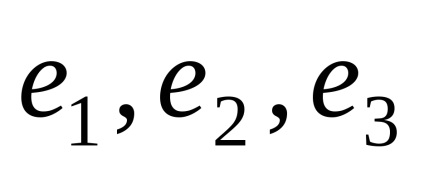
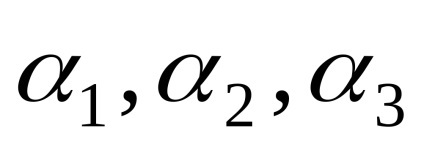

coordonatele vectoriale va scrie în acolade după vectorul simbol. De exemplu,
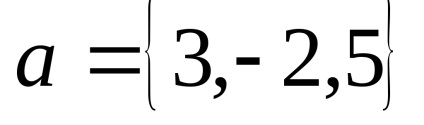

Din proprietățile multiplicării vectorului printr-un număr și adăugarea vectorilor afirmării în ceea ce privește operațiunile lineare asupra vectorilor care sunt coordonate definite.
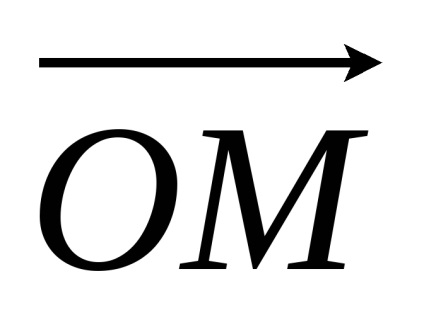
Pentru a găsi coordonatele vectorului, în cazul în care se știe coordonatele de început și de sfârșit, trebuie să fie de coordonatele corespunzătoare ale capătului său să ia de coordonate început.
operații liniare cu vectori numite adaos (scădere) a vectorilor și multiplicarea vectorului de către un număr. Să le examinăm.
vector OpredelenieProizvedeniem


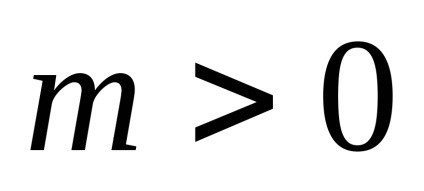

P
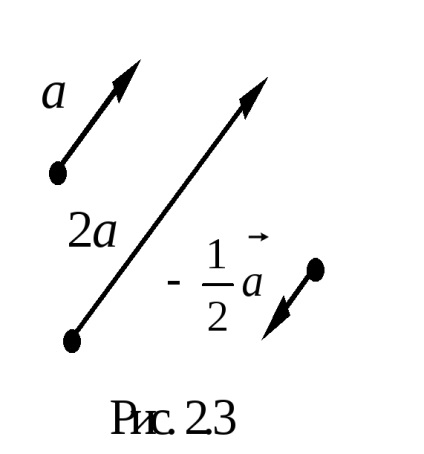
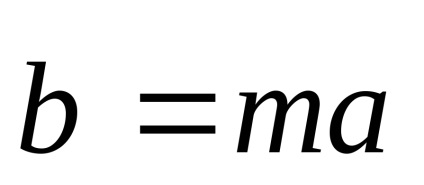
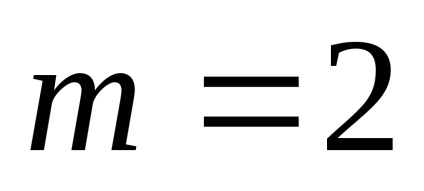
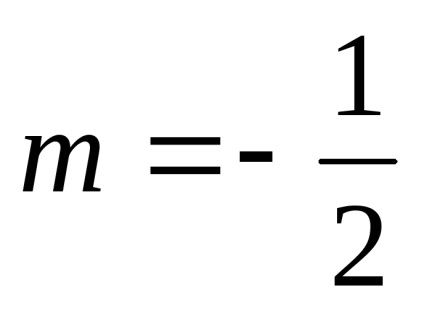
Când înmulțirea unui vector cu un număr de coordonatele sale sunt multiplicate cu acest număr.
Într-adevăr, în cazul în care
.
produs al vectorului

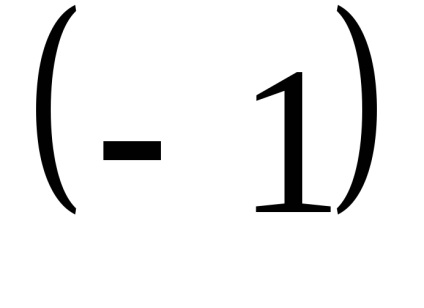
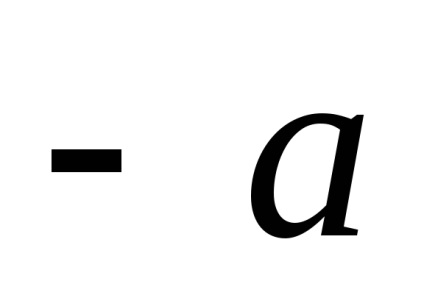
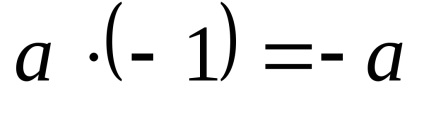

Rețineți că lungimea vectorului este egal cu 1, numită o unitate (sau unitate vector).
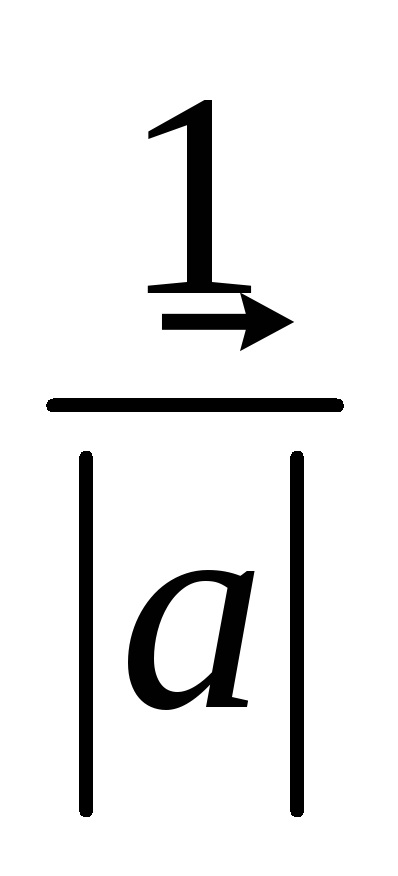
Utilizarea operație multiplicarea vectorului pe un număr, orice vector poate fi exprimat printr-un vector unitate în aceeași direcție. Într-adevăr, împărțirea vectorului



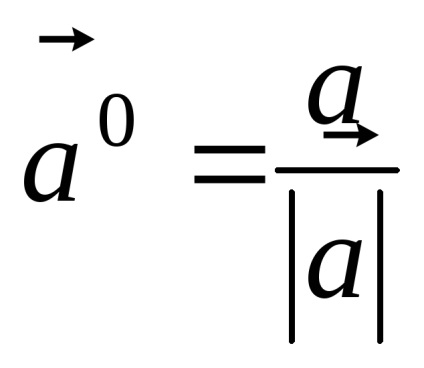
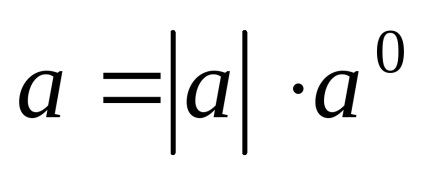
OpredelenieSummoy doi vectori



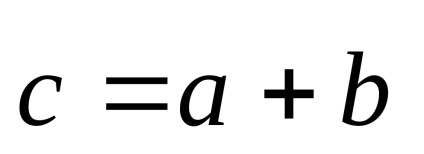
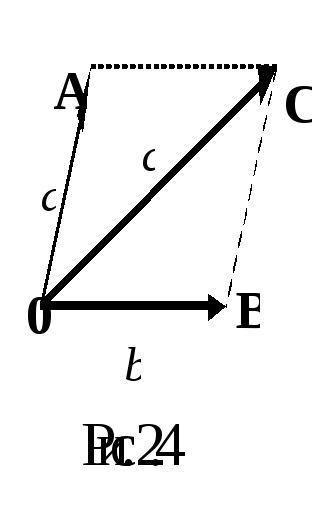
Prin definiție, vectori egali
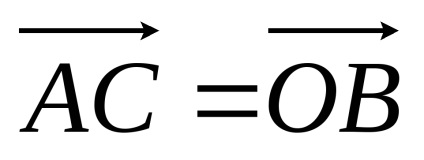


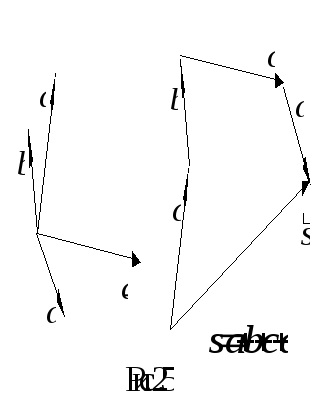
Deci, în scopul de a construi suma vectorială, este necesar să se atașeze la sfârșitul primului începutul vectorului de-al doilea, până la sfârșitul celei de a doua pentru a atașa la începutul celei de a treia, și așa mai departe. Apoi, suma vectorială și va fi un vector care se conectează la începutul primului dintre vectorii cu capătul acesteia din urmă.
Când se adaugă vectori adăugând și coordonatele lor corespunzătoare
Într-adevăr, în cazul în care,
Dacă vectorii