Etapa 2. Selectați obiectul de echilibru (acesta poate fi un nod, corpul de orice formă, structură complicată sau o parte a acestuia, mașini, unelte etc.).
Etapa 3. Afișarea predeterminate (cunoscute) forțele aplicate la echilibrul obiectului selectat.
Etapa 4. Stabilirea de conexiuni care acționează asupra obiectului, pentru a defini tipurile de conexiuni și arată reacția lor.
5 etape. Se determină tipul de sistem de forțe care acționează asupra unui obiect, și scrie pentru ecuațiile sale de echilibru (fiecare specie are propria ecuație).
6 etape. Urmați pașii prevăzuți de ecuațiile de echilibru (puterea de proiectare, pentru a calcula punctele lor, și așa mai departe), găsiți cantitățile dorite, rezultatele analizate.
Equilibrium sistem plan arbitrar al forțelor
Este necesar și suficient de echilibru al sistemului forțelor planar că suma forțelor pe cele două axe ale proeminențelor și suma cuplurilor cu privire la orice punct egal cu zero, adică
În loc de ecuațiile (9), este, uneori, mai bine să utilizați un alt sistem de ecuații
unde




unde


Pentru forțele de echilibru converg necesar și suficient ca suma acestor forțe ale proeminențelor de pe axele sunt zero, adică
Se determină fasciculul reacții de sprijin în cazul în care dimensiunea sa este cunoscută și circuitul de sarcină. grinzi de cântărire neglijate.
opțiuni de setare sunt prezentate în Fig. C 1-1 - Cu 1-2 și necesar pentru a aborda datele prezentate în tabelul. C 1.
Materializări 1 - 6 (Figura 3 C -. 1, C 3 - 2)
Determina AB fascicul de presiune pe suprafața de sprijin în cazul în care



Pe grinda în formă de U AB forță

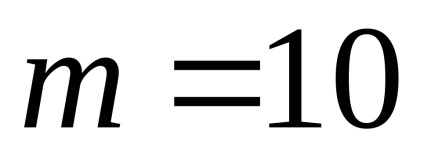


Se determină reacțiile de sprijin fascicul omogen AB cântărind 20 N, în cazul în care M = 10 Nm

AC și BC tije conectate pivotabil la punctul C. Se determină reacțiile de sprijin A și B. Dacă F = 15 H, m = 8 Nm


Fasciculul este conectat pivotabil cu AD BD rod imponderabilitate. Se determină reacții de sprijin A și B. Dacă F = 6 kN, m = 25 kN ° m,


La sfârșitul greutății uniformă pe orizontală a grinzii 8 kN este placa de beton omogen cu o greutate de 4 kN. Pentru a determina reacția etanșări A. Dacă F = 6 kN, M = 20 kN · m, AC = BD = CD = 2 m


Materializări 15 - 20 de (Figura 3 C - 6).
beam cantilever este supus unui cuplu forță cu momentul m = 16 Nm și intensitate distribuită sarcină q = 2 N / m. La capătul grinzii este suspendată de sarcină F = 30 N. Definiți terminare dacă reacția

Se determină reacții de sprijin A și fasciculul B prezentat în figură, în cazul în care F = 8 kN, m = 30 kN · m, q = 1,2 kN / m,
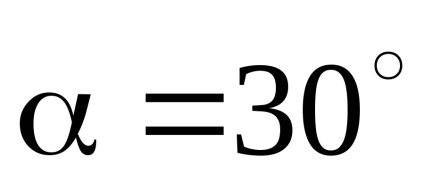
Se determină terminarea reacției grinzi rigide în formă de L ABC. dacă F = 6 kN, 10 kN = P,


Găsiți în formă de L reacții de sprijin fascicul AB, în cazul în care F = 5 kN, m = 30 kN · m, q = 0,9 kN / m,

Fascicolul omogenă AB cântărind 40 kN și 4 m reazemă capătul lung O proeminență în podea, iar nodul D intermediar bazat pe marginea pas. Se determină reacțiile de sprijin, în cazul în care


Omogeni fasciculului AB greutatea 25 N și o lungime de 6 m există un cuplu de forțe sub acțiunea unui cuplu de m = 8 Nm și uniform distribuit de intensitate a sarcinii q = 4 N / m, AC = BC. Se determină reacțiile de sprijin.

Determina AB grinzi presiune pe planurile de referință, dacă
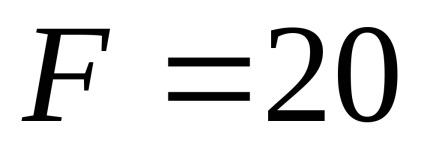
Se determină terminarea reacției grinzi rigide în formă de T, în cazul în care F = 15 H, q = 10, H / m, m = 14 H · m,

Se determină polii A și B de grinzi omogene de reacție AU 2 m lungime și greutatea acesteia dacă m = 15 H · m,

Se determină grinzile de susținere reacții A și B, în cazul în care q = 15, H / m, m = m H · 12, AC = 1 m, BC = 2 m

Se determină răspunsul și să sprijine o forță generată într-o tijă fără greutate Sun. dacă, F = 25 H, m = 10 H · m,

Se determină reacția de terminare a grinzii rigide AB, dacă F = 40 H, m = 18 H · m,
