Rezultatul elementar este termenul primar și poate fi explicată decât printr-un exemplu. Rezultatul Elemental este cea mai mică unitate indivizibilă de descriere a experimenta cel mai mic eveniment aleator. Se presupune că o experiență în același timp, nu se poate întâmpla sunt două rezultate elementare diferite. De exemplu,
1. Experiență: aruncarea unei monede
Rezultatele elementare: stema, cozi - doar două rezultate diferite
2. Experiență: aruncarea zaruri
Rezultatele elementare de realizare 1: numărul de puncte de pe fața superioară a rezultatelor -6
Rezultatele elementare Opțiunea 2: a scăzut chiar și cu fața sau impar -2 rezultat
3.Opyt: aruncarea a două zaruri
3.1 rezultate elementare de realizare 1: a scăzut într-o cantitate de 6 puncte sau a scăzut -2 rezultat
3.2 Rezultatele elementare Opțiunea 2: precipitații în cantitate de 7 puncte sau a scăzut -2 rezultat
3.3 Rezultatele elementare, opțiunea 3: suma punctelor scăzut - 11 rezultate ale
3.4 Elementar rezultatelor 4 opțiune: numărul de puncte de pe oase, fără discriminare zaruri [,,,,,,,,,,, ...] - 21 rezultat
3.5 elementar 5 rezultate realizare: numărul de puncte de pe oase, fără deosebire c [dice (1,1), (1,2), (1,3), (1,4), (1,5), (1, 6), (2,1), (2,2), ...] -36 rezultate
Spatiul rezultatelor elementare
Cardinality setului nu se măsoară în cai putere, iar numerele cardinale. Există seturi cu numărarea finit, cardinalitatea continuum, și chiar mai mult. În cazul în care elementele setului pot fi numărate, dar nu este definitivă, este numărabilă.
Setul de rezultate elementare ale unui experiment în teoria probabilității se numește spațiul de evenimente elementare. Rezultatele elementare sunt elemente (puncte) ale acestui set. În exemplele anterioare, este clar că poate fi comparat cu experiența reală a câteva descrieri de spațiu evenimente elementare. Astfel, pentru descrierea experimentelor ca setul principal de concepte matematice sunt folosite. În probabilităților sale partea generală nu utilizează niciun fel de proprietăți specifice ale evenimentelor elementare și seturi, cu excepția numărului de elemente din ele sau capacitatea lor. Prin urmare, orice spațiu de două evenimente elementare cu același număr de elemente sau aceeași putere din punctul de vedere al teoriei probabilității echivalente. De exemplu, în experiența de a arunca o monedă, putem alege ca rezultatele cuvântului „stema“ și „cozile“ sau numărul „0“ și „1“. Spațiul de evenimente elementare este, de obicei, după cum urmează:
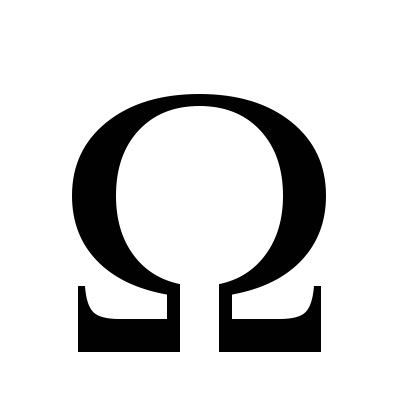
și el însuși ca un rezultat elementar

Puteți înregistra relația dintre spațiul de evenimente elementare si a rezultatelor, deoarece elementar
Sfaturi pentru construirea unui spațiu de evenimente elementare.
Rețineți problema pe care doriți să rezolve - este un eveniment aleator, probabilitatea de care aveți nevoie pentru a găsi, trebuie să fie descrise prin specificarea evenimentelor elementare care au condus la acest eveniment.
La început, încercați să introducă descriere mai detaliată a experienței - apoi începe să înțeleagă, în unele cazuri, este posibil, fără a aduce atingere rezultatului final, pentru a simplifica modelul.
Între diferite modele de model adecvat pare preferabil, în care rezultatele elementare sunt simetrice si la fel.
selectat Foarte convenabil rezultate elementare sub formă de vectori de dimensiuni egale cu numărul de diferiți factori aleatorii (surse) într-un fenomen aleator și coordonatele care corespund diferitelor valori candidate ale acestor factori. De exemplu, atunci când două zaruri aruncare rezultat elementar are dimensiunea 2 și 6 fiecare coordonată valori. Cu aruncarea simultană a monedei și osul unui vector este de dimensiune 2, valoarea primei coordonate a 2, al doilea - 6 (sau invers). În cazul în care moneda arunca 10, poate lua o multitudine de vectori binari diferite de dimensiune 10 de unu și zero ca spațiu de evenimente elementare.