oscilație de undă corespunzătoare, frecvența de oscilație
Propriile oscilații (libere) se numesc oscilații care au loc în sistem în absența influențelor externe și variabile se datorează deformarea inițială a unuia dintre parametrii sistemului din starea de echilibru. În sistemele macroscopice actuale, deoarece pierderea de energie amortizată întotdeauna oscilații libere.
Pentru mici abateri de la starea de echilibru a mișcării sistemului respectă principiul superpoziției. în care suma a două mișcări arbitrare este de asemenea mișcare admisibilă a sistemului; Este descrisă de mișcarea liniară (în particular, diferențiale) ecuații. În cazul în care sistemul este mai conservatoare și (nu există nici o pierdere sau flux de energie din exterior), și parametrii săi nu se schimbă în timp, atunci orice oscilație naturală poate fi reprezentat în mod unic ca o sumă de vibrații normale invariabilă sinusoidală în timp anumite frecvențe naturale.
În cazul în care poziția a sistemului, în orice moment poate fi descrisă printr-un singur parametru, sistemul are un grad de libertate. Exemple de astfel de sisteme de pendul. oscilant într-un plan predeterminat, masa asociată cu arc, LC-lant (Fig.1). Într-adevăr, poziția pendulului poate fi determinat unghiul pendulului de deflexie a firului din cp vertical. Pentru LC-lanț astfel parametru poate fi cantitatea de încărcare pe capacitate. (. Pendulum capabil să oscileze în orice direcție, cum ar fi Girs suspendat pe un fir, are două grade de libertate; avea nevoie de două coordonate pentru a determina pendulului poziție într-un ceas de perete este fixat astfel încât acesta poate pivota numai într-un anumit plan și, astfel, are un grad de libertate). .
Sisteme cu un singur grad de libertate
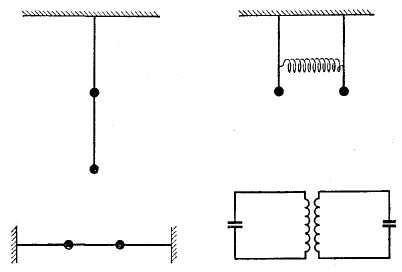
În natură există mai multe sisteme interesante cu două grade de libertate. Cele mai frumoase molecule exemple si particule elementare (K special neutru). Exemple mai simple sunt duble pendul (un pendul este suspendat din suport și oa doua întâi pendulului în greutate); două pendule. resort asociat; fir orizontal cu două bile; două LC-circuite cuplate (Fig. 2). Pentru a descrie starea de astfel de sisteme, sunt necesare două variabile. De exemplu,
în cazul unui pendul sferic, aceste variabile - o poziție pendulului în două direcții reciproc perpendiculare. În cazul pendule cuplate aceste variabile sunt în concordanță cu prevederile fiecăruia dintre pendulului; pentru două cuplate LC-circuite sunt taxele pe cele două recipiente sau curenții din cele două circuite.
Sistemul cu două grade de libertate
În general, mișcarea unui sistem cu două grade de libertate pot avea un aspect foarte sofisticat, nu ca o mișcare armonică simplă.
Timp de două grade de libertate și ecuațiile liniare ale mișcării de cele mai comune mișcarea este o superpoziție a două mișcări armonice simple, independente care apar simultan. Aceste doua mișcare armonică simplă se numește oscilații normale sau naturale și armonice, și modurile normale de vibrație, sau pur și simplu moduri.
In sistemele oscilatorii cu parametri concentrați constând din N cuplate oscilatoare (de exemplu, lanț oscilante circuite electrice sau conectate perle arcuri elastice), numărul de modul normal este egal cu N. Într-un sisteme parametru distribuit (string, diafragma sau rezonator po¬ly deschis) astfel de oscilații există infinit. De exemplu, pentru un șir cu fix capete o lungime L moduri diferă în numărul de jumătăți de valuri care pot fi stabilite pe toată lungimea șirului; L = nX / 2 (n = 0, 1, 2). Dacă viteza de propagare a undelor de-a lungul șirului este egal cu v. gama frecvențelor naturale este determinată prin formula
Dispersie wave Disponibilitatea (v = v (ω)) deformează acest simplu spectru de frecvență de distribuție kvazidistantnoe este deja determinată din ecuația de dispersie:
În sistemele reale, oscilațiile naturale vor fi amortizată din cauza pierderilor, astfel încât acestea să poată fi luate în considerare aproximativ armonice numai în intervalul de timp de mai puțin de 1 / δ. oscilațiilor damped poate fi reprezentat ca un pachet de frecvență de oscilație armonică umplere continuu interval (ω0 ± δω) (Fourier integrală), mai restrâns ö mai mic. În acest caz, el a spus extinderea liniilor spectrale, uneori, ce caracterizează factorul său Q egal cu raportul Q. pierderilor de energie W zarasennoy per perioadă de oscilație P 2π / ω. Astfel, condensarea spectrului datorită pierderilor presupune conversia spectrului discret în continuu când lățimea liniei devine aproximativ egală cu interval între ele.
Sistemele proprii Kolebaniyanelineynyh sunt mai puțin disponibile pentru clasificare. Sisteme de neliniaritate cu spectru discret conduce la transferul de modurile proprii de energie din componentele spectrale: astfel, există procese de concurență - modul de supraviețuire și suprimarea celuilalt. Dispersiile pot stabiliza aceste procese și să aducă la formarea structurilor spațiale și temporale stabile, ale căror exemple sunt solitoni în un sisteme de spectru continuu.
De o importanță deosebită în oscilație de excitație este un fenomen de rezonanță. care constă într-un răspuns creștere bruscă sistem (amplitudinea oscilațiilor) când frecvența forței externe la o anumită frecvență de rezonanță. caracterizarea sistemului. În cazul în care acesta din urmă este liniară și parametrii săi nu depind de timp, frecvența de rezonanță coincide cu oscilație sale naturale și răspunsul corespunzător al mai puternic, cu atât mai mare calitatea sistemului oscilatorii. Acumularea are loc atâta timp cât energia adusă din exterior (de exemplu, pentru fiecare abatere pendula) depășește pierderile în perioada de oscilație. Pentru vibrațiile liniare ale energiei primite de la sursa, este proporțională cu creșterea amplitudinii și a pierderilor proporțional cu pătratul ea, astfel încât echilibrul energetic este întotdeauna accesibil.
Este folosit în efecte științifice și tehnice
Măsurarea oscilațiile libere a produs în mod normal, pentru a obține informații cu privire la modurile și frecvențele, precum și viteza de oscilație de amortizare. Aceste măsurători sunt efectuate, de exemplu, testarea de zbor al aeronavei probe de cap, în care perturbația inițială generată de explozie de taxe mici. Un alt mod mai comun este de a muta brusc mânerele de control. Anterior, vibrațiile libere ale aeronavei în timpul testelor de la sol, uneori, excitat prin eliminarea rapidă a sarcinii statice. Cu ajutorul unei aripi frânghie întinsă dedus din poziția de echilibru; atunci coarda este tăiat, și ar putea fi observate oscilații libere.
Frecvențele și coeficienții de amortizare a formei oscilațiilor libere caracterizează de fapt, sistemul de „personalitate dinamică“. Deci, dacă avem suficiente informații despre aceste caracteristici ale sistemului, atunci putem spera că va fi posibil să se prevadă comportamentul sistemului în diferite condiții.
Sistemul de personalitate dinamică determină în mare măsură comportamentul său atunci când oscilații excitat. Sistemele mecanice se comportă ca și în cazul în care acestea sunt căutate în mod continuu pentru a face oscilații libere cu modurile proprii corespunzătoare. În condiții normale, acest lucru nu este posibil din cauza frecării, ci prin acțiunea unui oscilațiilor de conducere va fi menținută.
Oscilând de circuit - un circuit electric cuprinzând conectarea în paralel a unui inductor și un condensator. Într-un astfel de circuit poate fi excitat curent de oscilație (și tensiune).
Tensiunea din bobina atunci când curentul care trece este egal cu
În mod similar, pentru curentul cauzată de modificarea tensiunii pe condensator:
Din moment ce totul se produce în bobina de tensiune picături pe condensator, apoi uL = UC. un curent cauzată de condensatorul trece prin bobina, Reportofonul = iL. Diferențierea unul dintre ecuațiile și înlocuind rezultatul în celălalt, obținem
Acest oscilator armonic ecuație cu frecvență unghiulară
(În caz contrar, se numește frecvența naturală a oscilatorului armonic). Soluțiile acestei ecuații este
Luați în considerare proprietățile de vibrație ale pendulului elastic, care este un material punct de masă m. conectate fără greutate rigiditate arc k din suspensia fixă (Fig.1).
Să L0 - lungimea arcului de stat nenagruzhonnom. În cazul în care arcul de a suspenda masa m de sarcină. arcul de gravitație este întinsă și lungimea sa devine egală cu l. Dacă sarcina și arcul sunt în echilibru, forța gravitațională este echilibrată de forța elastică. Numărarea coordonatele punctului material din poziția de echilibru. Ecuația arc de mișcare poate fi scrisă ca
- frecvența vibrațiilor naturale sau a frecvenței naturale neamortizate.
Teoria vibrațiilor 1. Migulin V.VOsnovy M. Nauka, 1978.
2. Teodorchik KF Sisteme de oscilatorii AM Gostekhizdat 1952.
3. Gunners SP Introducere în teoria oscilațiilor științei 1964.
Este nevoie de frame-uri inline de sprijin.