Curs 15. Suprafețele de ordinul al doilea.
În ecuația formează spațiul tridimensional definește o suprafață. Deci, noi știm deja ecuația suprafeței primei comenzi - avionul.
O ecuație algebrică a doua și superioare comenzilor din spațiul definește suprafețele care sunt numite suprafețele a doua și superioare comenzilor. Să considerăm ecuația suprafeței Quadric și protozoare.
Suprafață de revoluție este o suprafață formată prin rotirea unei linii L spațială (numită formare) cu privire la o predeterminată linie dreaptă l (numita axa de rotație), situată în același plan L (figura 1).
Evident, în timpul rotației sale L fiecare punct descrie un cerc.
Cel mai simplu caz al unei suprafețe de revoluție, curba L este rotit în jurul axelor de coordonate.
Suprafețele formate prin rotirea unei a doua curbe de ordine în jurul axei lor de simetrie, numite suprafețe de ordinul doi de revoluție.
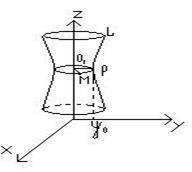
Fie S - suprafața de revoluție, M (x y z ..) - un punct arbitrar al suprafeței. Desenează un plan de Oz. care trece prin punctul de punctul M. Fie O1 de intersecție a planului cu Oz. P și punct - o curbă L. Apoi O1 (0,0, z) și P (. 0, y0 z), unde y0 - unele număr.
Avionul în secțiune a unui S suprafață obținută printr-un cerc; punctul P și M se află pe acest cerc și raza cercului este egal cu | O1 M | = | O1 P |. Au | O1 P | = | y0 | (Deoarece LÎy Oz), apoi pe de o parte O1 M | = | y0 |. În același timp,
În consecință, | y0 | =. sau y0 = ±. Deoarece PÎL, atunci coordonatele sale satisfac curba ecuații. prin urmare, F (y0, z) = 0. Reprezentarea aici y0 = ±. obținem
înseamnă coordonatele unui punct M (x y z ..), situată pe o suprafață de rotație satisface ecuația F = (±; z) = 0, atunci această ecuație este ecuația suprafeței S.
In mod similar, se poate obține o suprafață ecuație de rotație în jurul altor axe.
Din aceasta putem deduce urmatoarea regula:
Pentru a găsi ecuația de suprafață a curbei L de rotație în jurul axelor de coordonate situate într-un același plan L, este necesar ca în curba ecuație L variabilă care corespunde axului de rotație, rămân neschimbate. și oa doua variabilă este înlocuită cu (±) rădăcina pătrată a sumei pătratelor variabilelor rămase.
De exemplu, dacă L: (. X y) F = 0, LÎx Oy și se rotește în jurul axa Oy. Suprafața Eq de rotație F = (±; z) = 0. Dacă curba este rotit în jurul axei Ox. ecuația de suprafață este scrisă sub forma F = (x; ±) = 0. Dacă L: F (x z.) = 0 este rotit în jurul Oz. atunci suprafața are o ecuație F = (±; z) = 0 etc.
De exemplu, dacă circumferința de rotație (y - a) 2 + z 2 = 1 se va transforma în jurul axei Oy mingea, iar când acesta este rotit în jurul axei OZ - (. Fig) Torul
Această suprafață se numește două coli hiperboloid de rotație. Dacă deforma, vom obține un hiperboloid cu două sub formă de foaie
Distincții: 3 pătrat minus 2, cea din dreapta.
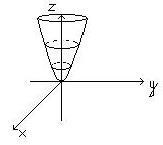
3) Să considerăm parabolei y 2 = 2pz și se va roti în jurul axei sale Oz. Obținem o suprafață cu ecuația x 2 + y 2 = 2pz. sau rotație -paraboloid.
Fie L - o anumită linie în spațiu, și l - drepte, nu mint cu L în același plan.
Suprafața cilindrică este o multitudine de puncte în spațiu, care este unirea tuturor liniilor drepte paralele cu linie dată l și care trec prin punctul de pe curba L. Linia L se numește ghidajul, iar liniile paralele cu linia l - formarea cilindru.
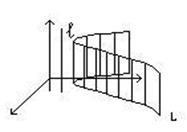
Să considerăm o suprafață cilindrică având generatoarele paralele cu axele și ghidajele, situată în coordonate plane.
Fie L: - curba în spațiu (în mod evident, acesta se află în planul x Oy), și l = Oz.
Luați în considerare o suprafață cilindrică. Fie M (x y, z.) - un punct arbitrar al suprafeței. Apoi proiecția M1 (x y 0 ..) Din acest punct de pe x Oy se află pe un plan de ghidare L. Prin urmare, coordonatele x și y sale satisfac ecuația L:
Invers, în cazul în care punctul N (x1. Y1. Z1) nu aparține suprafața cilindrică, atunci F (x1. Y1) ¹ 0 (N ÏL), adică ecuația F (x. Y) = 0, coordonatele punctelor întâlnesc suprafața cilindrică și numai ei, prin urmare, F (x. Y) = 0 este ecuația suprafeței de ghidare cilindric și o generatoarei paralelă cu Oz.
In mod similar se poate demonstra că ecuația F (x, z) = 0 definește o suprafață cilindrică cu generatoarea paralelă cu Oy și ghidajul
Ecuația F (y, z) = 0 definește o suprafață de ghidare cilindrică și o generatoarei paralelă cu axa Ox.
Suprafața cilindrică în care ghidajul are o curbă de ordinul 2 se numește suprafața cilindrică a două ordine.
De exemplu, suprafața (sau) este un cilindru parabolic.
Ecuația de suprafață sau - un cilindru eliptic:
Ecuațiile și să definească cilindru hiperbolic: