luând în considerare, în general, orice unghiuri cu laturile paralele respective sau cu laturi perpendiculare, respectiv. Luați în considerare primul caz.
două unghiuri ABC și DEF sunt lăsați. laturile lor sunt paralele: AB || DE și BC || EF. Aceste două unghiuri sunt fie egale sau suma lor va fi egală cu 180 °. Următoarea figură, în primul caz ∠ABC = ∠DEF, iar în al doilea ∠ABC + ∠DEF = 180 °.

Dovada că aceasta este într-adevăr cazul, este următoarea.
Luați în considerare unghiuri cu laturile paralele, respectiv, situate atât în prima imagine. În același timp, extinde liniile AB și EF înainte de a traversa. Notăm prin punctul de intersecție G. Mai mult decât atât, pentru claritate, dovezi suplimentare ale figura extinse din partea BC.
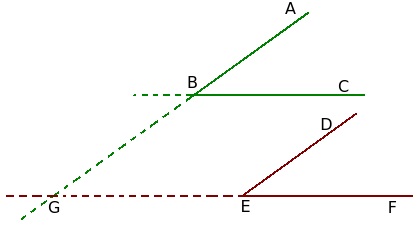
Deoarece liniile BC și EF sunt paralele, în cazul în care linia AB intersectează una dintre ele, atunci acesta trebuie să treacă, și alta. Asta este, linia AB este secțiunea transversală a două linii paralele. După cum se știe, în acest caz, minciună se intersectează în cruce la unghiuri egale sided adăuga până la 180 °, corespunzător egal.
Aceasta este ceea ce un cuplu de colturi avem la B și a vârfurilor G (un unghi una față de alta de-al doilea), obținem întotdeauna fie unghiuri egale, sau de a da un total de 180 °.
Cu toate acestea, liniile AB și DE sunt, de asemenea, paralele. Pentru ei este o FE directă - este transversală. Prin urmare, orice pereche de vârfuri ale unghiurilor G și E va fi suma fie de 180 °, fie egale între ele. De aici rezultă că unghiurile perechii de noduri B și E se vor supune această regulă.
De exemplu, ia în considerare unghiurile ∠ABC și ∠DEF. Unghiul ABC egal cu unghiul BGE, deoarece aceste unghiuri la linii paralele respective BC și EF. La rândul său, unghiul de BGE egal cu unghiul DEF, deoarece aceste unghiuri sunt, respectiv paralel cu AB și DE. Astfel, se dovedește, ∠ABC și ∠DEF.
Acum, să ne ia în considerare unghiurile ∠ABC și ∠DEG. unghi ABC egal cu unghiul BGE. Dar ∠BGE și ∠DEG - este unghiuri unilaterale de linii paralele (AB || DE), străbătute de intersectându (EF). După cum se cunoaște, aceste unghiuri adăuga până la 180 °. Dacă ne uităm la al doilea caz, în prima imagine, ne dăm seama că aceasta corespunde unei perechi de unghiuri și ABC ° în a doua imagine.
Astfel, cele două unghiuri diferite, ale căror laturi sunt, respectiv paralele sau egale între ele, sau de a adăuga până la 180 °. Acest lucru dovedește teorema.
Trebuie remarcat un caz special - atunci când unghiurile dislocate. În acest caz, ei vor în mod evident, egale între ele.
Acum ia în considerare unghiurile cu laturile perpendiculare, respectiv. Acest caz este mai complicată, deoarece poziția relativă a unghiurilor variate. Figura de mai jos trei exemple de modul în care unghiurile pot fi aranjate cu laturile perpendiculare, respectiv. Cu toate acestea, în orice caz, o parte a primului unghi (sau extinderea acesteia) este perpendicular pe o parte a doilea unghi, iar cea de a doua parte a primului unghi perpendicular pe a doua latură a doilea unghi.
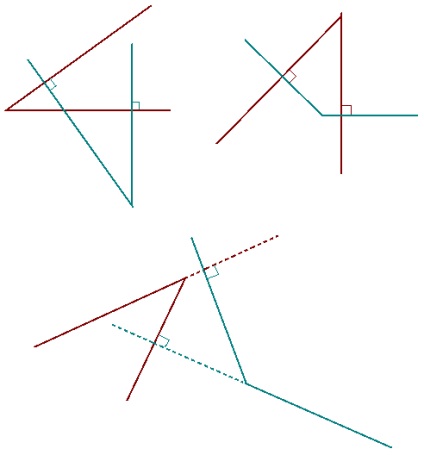
Luați în considerare unul din cazuri. Astfel, într-un unghi de așteptare bisectoare și care trece printr-un punct arbitrar va organiza perpendiculare pe laturile colțul său.

Aici sunt unghiurile ABC și DEF, respectiv, cu laturile perpendiculare: AB ⊥ DE si BC ⊥ EF. Pe bisectoarea unghiului ABC pentru a lua un punct de G, care se realizează perpendicularele la același colț: GH ⊥ AB si GI ⊥ BC.
Luați în considerare triunghiuri BGH și BGI. Ele sunt rectangulare, deoarece acestea au unghiurile H și I directe. Acestea au inclus unghiurile B sunt BG - bisectoarea unghiului ABC. De asemenea, triunghiuri luate în considerare partea BG este ipotenuza și totalul pentru fiecare dintre ele. După cum știți, triunghiurile sunt egale, dacă acestea sunt egale cu ipotenuza și unul dintre unghiurile acute. Astfel, ΔBGH = ΔBGI.
Deoarece ΔBGH = ΔBGI, The ∠BGH = ∠BGI. De aceea, unghiul HGI poate fi prezentat nu ca o sumă a acestor două unghiuri, și unul dintre ei înmulțit cu 2: ∠HGI = * 2 ∠BGH.
Unghiul ABC poate fi scris ca suma a două unghiuri: ∠ABC = ∠GBH + ∠GBI. Deoarece termenii unghiurile sunt egale între ele (.. M pentru a forma bisector), unghiul ABC poate fi reprezentat ca produsul unuia dintre ei și de 2: ∠ABC = ∠GBH * 2.
Unghiurile BGH și GBH - este unghiuri ascuțite ale unui triunghi dreptunghic, și apoi se adaugă până la 90 °. Să ne uităm la capitaluri proprii, care pot fi obținute:
∠BGH + ∠GBH = 90 °
∠HGI = ∠BGH * 2
∠ABC = ∠GBH * 2
ultimele două pliului:
∠HGI + ∠ABC = ∠BGH * 2 + ∠GBH * 2
Eliberat un factor comun pentru consola:
∠HGI + ∠ABC = 2 (∠BGH + ∠GBH)
Deoarece suma unghiurilor în paranteze este de 90 °, atunci se dovedește că unghiurile HGI și ABC în cantitate de până la 180 °:
∠ABC + ∠HGI = 2 * 90 ° = 180 °
Deci, am demonstrat că suma unghiurilor HGI și ABC este de 180 °. Acum, uita-te din nou la imaginea și să se întoarcă atenția la unghiul cu care unghiul ABC, respectiv, perpendicular pe lateral. Acest unghi DEF.

GI directă și EF paralele între ele, deoarece acestea sunt ambele perpendiculare pe aceeași linie dreaptă BC. Și, după cum știți, linii drepte care sunt perpendiculare pe aceeași linie dreaptă, paralele între ele. Din același motiv, DE || GH.
Ca unghiuri anterior fost deja dovedite cu laturile paralele sau, respectiv, se adaugă până la 180 °, sau egale între ele. Aceasta înseamnă că, fie ∠DEF = ∠HGI sau ∠DEF + ∠HGI = 180 °.
Cu toate acestea ∠ABC + ∠HGI = 180 °. De aici concluzia că, în cazul respectiv, laturile perpendiculare sau colțuri sunt egale, sau pentru a adăuga până la 180 °.
Cu toate că, în acest caz, avem doar dovezi limitate din suma. Dar dacă mental extinde EF spre direcția opusă, vom vedea unghiul care este egal cu unghiul ABC, și, astfel, de asemenea, perpendicular pe ABC său de colț lateral. Dovedirea egalitatea unghiurilor este posibilă, având în vedere unghiurile, respectiv, cu laturile paralele: ∠DEF și ∠HGI.