Pregătirea elevilor pentru examenul la rezoluția centru de formare (manual de matematică - elementele

• Obiectivele de interes
• trinom pătratic
• Ecuații și Inegalitățile
  cu module
• Aritmetice și geometrice progresii
• metoda de coordonate
  în avion
• Cifrele pe un plan de coordonate definit de inegalitățile
• Soluție de ecuații algebrice
• Soluția inegalităților raționale
• Decizia de inegalitățile iraționale
• Soluție de ecuații exponențială
• demonstrație Soluție inegalităților
• Soluție ecuații logaritmice
• Soluție inegalitățile logaritmice
• sistemul de ecuații
• Soluție de ecuații trigonometrice
• Trigonometrie în examen
  în matematică
• Gradul cu exponent rațional

MATERIALE INSTRUCȚIONAL OFICIALE

caracteristici limitate și nelimitate

Fie X un set de numere litere care apar în domeniul D (f) funcția y = f (x).

1. Determinarea funcției y = f (x) se numește o limită superioară X. set Dacă există un număr de. că, pentru fiecare din multitudinea de x satisface inegalitatea X

2. Determinarea funcției y = f (x) se numește mărginită de mai jos pe X. set Dacă există un număr b. că, pentru fiecare din multitudinea de x satisface inegalitatea X

3. Determinarea funcției y = f (x) se numește mărginită pe X. Dacă există și b. că, pentru fiecare din multitudinea de x satisface inegalitatea X

4. Determinarea funcției y = f (x) se numește un set unbounded deasupra X. Dacă pentru orice număr există o multitudine de astfel de x X. pentru care inegalitatea

5. Determinarea funcției y = f (x) este numit nerestricționată de mai jos pe X. set Dacă pentru orice număr b există o pluralitate de X. x pentru care inegalitatea

6. Determinarea funcției y = f (x) este numit pe X. set nelimitat în cazul în care această funcție sau unbounded deasupra sau dedesubtul unbounded sau unbounded de sus și de jos.

Noi ilustrează aceste definiții exemplele care urmează.

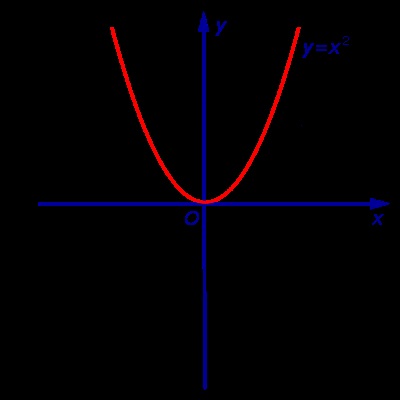
Exemplul 1. Funcția y = x 2 (Fig. 1) este limitată de mai jos și pe partea de sus a setului nelimitat

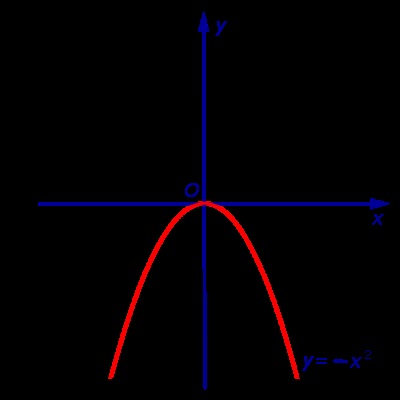
Exemplul 2. Funcția y = - x 2 este mărginită deasupra și dedesubt printr-o pluralitate de unbounded (Figura 2).

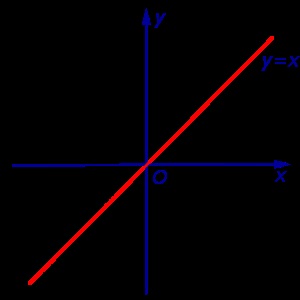
Exemplul 3. Funcția y = x (Fig. 3) nu delimitate deasupra și dedesubt printr-o pluralitate de unbounded

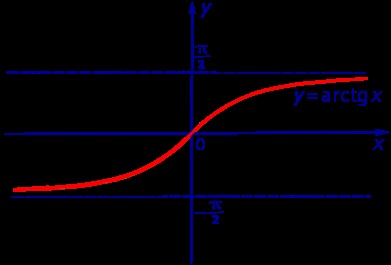
Exemplul 4. Funcția y = arctg x (Fig. 4) delimitat

funcții monotone și strict monotone

7. Determinarea funcției y = f (x) este numit pentru creșterea X. set Dacă pentru orice numere și satisface inegalitatea x1

Observația 1. Funcția de creștere este numit, de asemenea, funcții non-descrescătoare.

8. Determinarea funcției y = f (x) este numit pentru descreșterea X. set Dacă pentru orice numere și satisface inegalitatea x1

Notă 2. Funcția Atenuarea este numit, de asemenea, funcții non-creștere.

9. Determinarea funcției y = f (x) se numește strict în creștere pe X. Dacă pentru orice set de numere și care satisface inegalitatea x1

10. Determinarea funcției y = f (x) se numește strict descrescătoare pe X. set Dacă pentru orice numere și satisface inegalitatea x1

Definiție 11. Creșterea și scăderea funcției se numește monotonă. strict crescătoare și funcții strict descrescătoare se numește strict monotonă.

Exemplul 5 Funcția y = x 2 (Fig. 1) este strict scăderea funcției pe un set de strict crescătoare pe set

Exemplul 6. Funcția y = - (. Figura 2) x 2 este o funcție strict crescătoare pe platourile de filmare și setul strict descrescătoare

Exemplul 7. Funcția y = x (fig. 3) este o funcție strict crescătoare pe platourile de filmare

Exemplul 8. Funcția y = arctg x (Fig. 4) este strict crescatoare pe platourile de filmare

Chiar și impare funcții

12. Determinarea funcției y = f (x). definite pe X. set numit chiar funcție dacă, pentru orice număr x din numărul setat X - x, de asemenea, aparține setului X și egalitatea

13. Determinarea funcției y = f (x). definite pe X. set numit funcție ciudat, dacă pentru orice număr x din numărul setat X - x, de asemenea, aparține setului X și egalitatea

Exemplul 10. Exemple de caracteristici care nu sunt nici măcar, nici funcții impare. sunt funcții exponențiale și logaritmice.

Aprobarea. Orice funcție y = f (x). simetrice în raport cu un anumit punct set x = 0 X. poate fi reprezentat ca suma pare și impare funcții.

Dovada. Luați în considerare două funcții:

suma care este egală cu f (x). și observăm că funcția g1 (x) este o funcție chiar și funcția g2 (x) este o funcție ciudat. De fapt,

care completează dovada.

Notă 3. Extinderea funcției y = e x în sumă de funcții pare și impare, obținem:

o g1 funcție (x) este numită cosinusul hiperbolic și reprezintă ch x.

O g2 funcție (x) este numit sinus hiperbolic si denota sh x.

Astfel, egalitatea

Funcții periodice și neperiodice. elemente de epocă

14. Determinarea numărului numit perioada funcției f (x). dacă pentru orice număr de și x + T x - T, de asemenea, fac parte din domeniul D (f) și egalitățile

Definiție 15. Dacă funcția are o perioadă, atunci aceasta se numește periodică. Dacă în momentul în care funcția este nu, atunci aceasta se numește non-periodice.

Notă 4. În cazul în care numărul T este perioada unei anumite funcții, numărul și kT. unde k - orice număr întreg altul decât zero, cum este perioada funcției.

Exemplul 11. Funcții y = sin x și y = cos x sunt funcții periodice cu perioada 2π. funcției y = tg x și y = ctg x sunt funcții periodice cu perioada π.

Graficul functiei. Proprietăți grafice, chiar și funcții impare, periodice

16. Determinarea funcției Schedule y = f (x) este multimea tuturor punctelor ale căror coordonate sunt de forma (x; f (x)). în cazul în care.

Figura 6. Notă funcția periodică nu este modificată prin deplasarea de-a lungul axei Ox a abscisa perioada spre dreapta sau spre stânga (a se vedea. De exemplu, secțiunea „graficele funcțiilor trigonometrice“ referința noastră). Prin urmare, pentru a construi un grafic al unei funcții periodice cu perioada T. suficientă pentru a construi graficul acestei funcții la orice interval axa abscisei Ox lungime T. și apoi mutați-l la stânga și la dreapta de distanța nT. unde n - orice număr întreg.

Puteți obține, de asemenea, cunoștință cu profesorii dezvoltat un centru de formare „rezolutiv“ materiale de instruire pentru a se pregăti pentru examenul la matematică.

Pentru studenții care doresc să se pregătească bine pentru și promovat examenul la matematică, fizică sau limba română pentru un scor mare, centrul de formare „rezolutiv“ deține

articole similare

• Pregătirea studenților pentru examenul și OGE (DPA), în rezoluția centru de formare (manual de matematică -