Momentul unei forțe în jurul unui punct O - este un vector al cărui modul de elasticitate este egal cu produsul modulului de alimentare pe umăr - cea mai mică distanță de la punctul O la linia de forță. Direcția forței unghiulare vectorul impuls perpendicular pe planul care trece prin punctul și linia de acțiune a forței, astfel încât în căutarea în direcția vectorului momentului unghiular, rotația, comise prin forță în jurul punctului O, este sensul acelor de ceasornic.
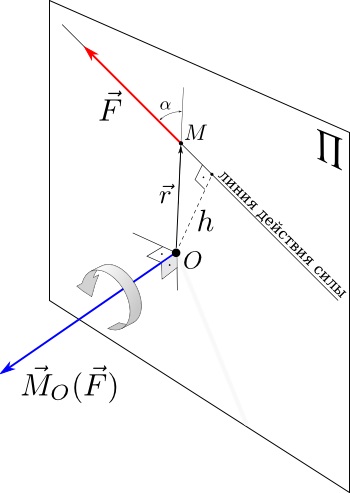
Dacă știți vectorul rază $ \ r $ vec punctul de aplicare a forței de $ \ vec F $ în ceea ce privește punctul O, momentul acestei forțe despre O este exprimată după cum urmează:
$$
\ Vec M_O (\ F vec) = \ r \ vec ori \ vec F.
$$
Într-adevăr, un modul al produsului vectorial:
$$
| \ Vec M_O | = | \ R \ Vec ori \ F vec | = | \ Vec r | | \ Vec F | \ Sin \ alpha.
$$
În conformitate cu figura $ | \ r vec | \ păcat \ alpha = $ h, astfel:
$$
| \ Vec M_O | = | \ Vec F | h.
$$
Vector $ \ vec M_O $, ca rezultat al produsului vectorial, vectori perpendiculari $ \ vec r $ și $ \ vec F $, plan care aparțin \ Pi $. Direcția vectorului $ \ vec M_O $ este de așa natură încât căutarea în direcția vectorului, cea mai scurtă rotație de la $ \ vec r $ la $ \ vec F $ este în sens orar. Cu alte cuvinte, vectorul $ \ vec M_O $ completează sistemul de vectori $ (\ r vec, \ vec F) $ la trei dreapta.
Cunoscând coordonatele punctului de aplicare a forței într-un sistem de coordonate a cărui origine coincide cu punctul O, și proiecția forțelor pe axa de coordonate, momentul forței poate fi definită după cum urmează:$$
\ Vec M_O = \ r \ vec ori \ F = vec
\ începe
\ Vec I \ Vec j \ Vec k \\
x y z \\
F_x F_y F_z
\ End = (y F_z - z F_y) \ vec i + (z F_x-x F_z) \ vec j + (x-y F_y F_x) \ vec k.
$$
Momentul unei forțe în jurul unei axe
Proiecția momentului de forță cu privire la un punct de pe o anumită axă care trece prin acest punct se numește momentele de forță în jurul axei.
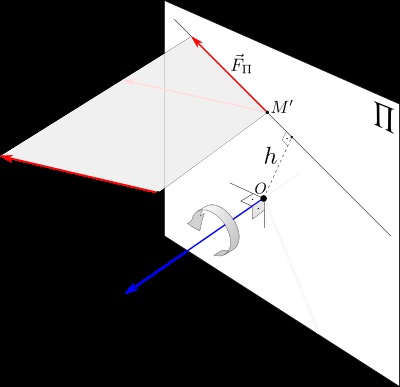
Momentul de forță în raport cu axa este calculată ca fiind timpul de proiecție a forței de $ \ vec F $ pe planul $ \ Pi $, perpendicular pe axa, în raport cu punctul de axa de intersecție cu avionul $ \ Pi $:
$$
M_z (\ vec F) = M_z (\ vec F_ \ Pi) = \ pm F_ \ Pi h.
$$
moment al semnului determinat de direcția de rotație, care tinde să dea organismului puterea de $ \ vec F_ \ Pi $. Atunci când se uită în direcția axei Oz $ $ forța se rotește în momentul în corpul sensul acelor de ceasornic este luat cu semnul `` plus „“, sau - `` negativ „“.