viteza unghiulară Ω a corpului în acest punct se numește limite de traiectorie circulară (la → 0 DT) a raportului de deplasare mici unghiulare δφ la interval de timp mic AT:
Viteza unghiulară se măsoară în rad / s.
Comunicarea între modul și viteza liniară υ ω viteza unghiulară:
În mișcare uniformă a unui corp circumferențiare υ și w valorile rămân neschimbate. În acest caz, vectorul de mișcare doar schimbă direcția
mișcarea uniformă a corpului este circumferențial mișcare cu accelerație. accelerare
este orientată radial spre centrul cercului. Se numește accelerație normală sau centripetă. Modul de accelerație centripetă asociată cu viteze unghiulare w relații liniare υ și:
Pentru a dovedi acest lucru, să ia în considerare modificarea expresiei vectorului de viteză pentru o perioadă mică de timp dt. Prin definiție, accelerarea
accelerația centripetă a corpului cu o mișcare circulară uniformă
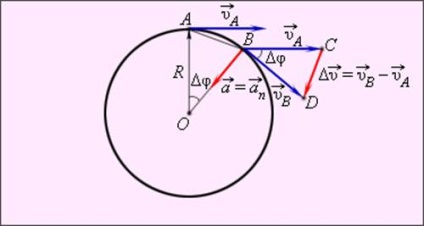
Vectorii de viteză și punctele A și B sunt orientate de-a lungul tangentei la cerc la aceste puncte. module egale cu viteze υA = υB = υ.
Din similitudinea triunghiurilor OAB și BCD ar trebui să fie (Figura 1.6.2.):
Pentru valori mici ale unghiului δφ = distanța ωδt | AB | = Δs ≈ υδt. Din moment ce | OA | = R și | CD | = Δυ, din similitudinea dintre triunghiuri din Fig. 1.6.2 obținem:
La unghiuri mici δφ direcția vectorului se apropie de direcția centrului cercului. Prin urmare, trecerea la limita ca → 0 AT, obținem:
La schimbarea poziției corpului pe cercul schimbă direcția centrului cercului. În mișcare uniformă a unui modul de accelerare circumferențial corpul rămâne neschimbat, dar direcția vectorului accelerație variază în funcție de timp. Vector Accelerația la orice punct al cercului este îndreptat spre centrul său. Prin urmare, la mișcarea accelerație uniformă a corpului numit circumferențial centripetă.
In vectorul formează accelerația centripetă poate fi scrisă ca
în care - vectorul raza unui punct de pe cerc, începutul care este în centrul său.
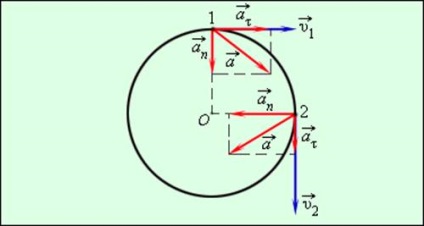
În cazul în care corpul se mișcă într-un cerc inegale, atunci există, de asemenea, tangentă (sau tangențial), componentă a accelerației (a se vedea 1.1):
În această formulă δυτ = υ2 - υ1 - modifica viteza modulului în timpul timpului dt interval.
Direcție vector accelerație completă se determină la fiecare punct al valorilor circulare ale traiectoriei accelerațiile normale și tangențiale (Fig. 1.6.3).