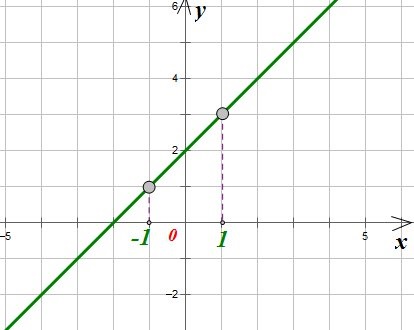
1. Plot funcția dacă se știe că acesta trece prin punctul A (-3, 2) și paralel cu linia dreaptă y = -4x.
Funcția Ecuația doi parametri necunoscuți: k a și b. Prin urmare, în textul celor două condiții trebuie să fie obiective ce caracterizează graficul funcției.
a) Din faptul că graficul paralel linie y dreaptă = -4x, rezultă că k = -4. Care este ecuația funcției are forma
b) Rămâne de a găsi b. Este cunoscut faptul că graficul funcției trece prin punctul A (-3, 2). În cazul în care punctul aparține graficul funcției, apoi prin substituirea coordonatele sale în funcțiile de ecuație, obținem adevărata egalitate:
Astfel, avem nevoie pentru a construi un grafic al funcției
Punctul A (-3, 2), este cunoscut, ia un punct B (0, -10)
Am pus aceste puncte în planul de coordonate, și să se alăture ei printr-o linie dreaptă:
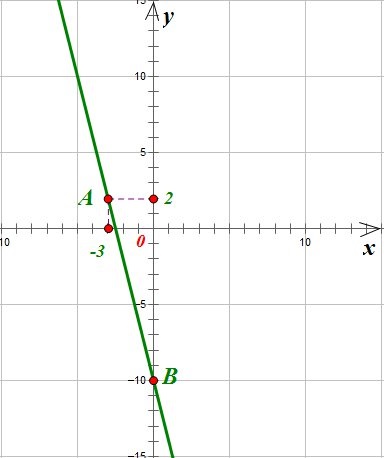
2. Scrieți ecuația liniei ce trece prin punctele A (1, 1); B (2, 4).
Dacă linia trece printr-un punct cu coordonatele date, prin urmare, coordonatele punctelor satisfac drepte ecuație. Adică, dacă vom înlocui coordonatele punctelor în ecuația liniară, obținem adevărata egalitate.
Coordonatele substitutive fiecărui punct în ecuație și un sistem de ecuații liniare.
Scăzând prima și obține din a doua ecuație. Substituind valoarea k în prima ecuație și obține b = -2.
Astfel, ecuația liniei.
3. Se trasează ecuația
Pentru a afla pentru ce valori ale produsului necunoscut de mai mulți factori este zero, este necesar să se echivaleze fiecare factor la zero și uchestODZ fiecare factor.
Această ecuație nu este limitată la DHS. Noi factorize a doua categorie și echivala fiecare factor la zero. Se obține un set de ecuații:
Noi construim un grafic al tuturor ecuațiile împreună într-un singur plan koordnatnoy. Acesta este graficul ecuației:
Nu vom construi un program, găsiți doar ecuația liniei.
a) Deoarece graficul funcției. în cazul în care este perpendicular pe linia. Prin urmare. aici. Care este ecuația funcției are forma
b) Știm că graficul M trece prin punctul (-1, 2). Înlocuim coordonatele sale în funcția de ecuație. obținem:
Prin urmare, funcția noastră este după cum urmează :.
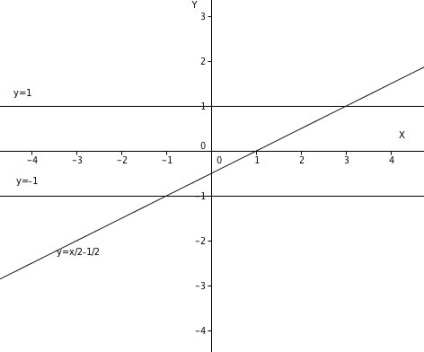
5. Construirea unui grafic al funcției
Noi simplifica expresia de pe partea dreaptă a ecuației funcției.
Important! simplifica înainte de expresie, vom găsi DHS.
Numitorul fracției nu poate fi zero, deci -1 „title =» x<>-1 „/>.
Apoi, funcția noastră ia forma:
și împungere l două puncte cu abscisă x = 1 și x = -1: